Question

13．①在[0，4]內隨機取兩個數a，b，則使函數f（x）=x²+ax+b²有零點的概率為$\frac{1}{4}$．
②在△ABC中，“$\overrightarrow{AB}$•$\overrightarrow{AC}$＞0”是“△ABC為銳角三角形”的充要條件
③已知x＞-1，y＞0且滿足x+2y=1，則$\frac{1}{x+1}$+$\frac{2}{y}$的最小值為$\frac{9}{2}$
④已知點P為△ABC所在平面上的一點，且$\overrightarrow{AP}$=$\frac{1}{3}$$\overrightarrow{AB}$+t$\overrightarrow{AC}$，其中t為實數，若點P落在△ABC的內部，則t的取值范圍是0＜t＜$\frac{2}{3}$其中正確的有①③④．

Answer 1

分析 ①為幾何概型問題，求出區域D，d，以面積為測度，計算即可判斷；
②由向量的數量積的定義和充分必要條件的定義，即可判斷；
③將$\frac{1}{x+1}$+$\frac{2}{y}$轉化為$\frac{1}{x+1}$+$\frac{4}{1-x}$（-1＜x＜1），再由基本不等式可得最小值，即可判斷；
④用向量的加法法則，用以A為起點的向量表示得到$\overrightarrow{AP}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$，畫出圖形，結合點P落在△ABC的內部從而得到結論．

解答 解：①為幾何概型問題．區域D：0≤a≤4，0≤b≤4，
函數f（x）=x²+ax+b²有零點的條件為△≥0，即a²-4b²≥0，
即有區域d：a-2b≥0，畫出區域D，d，
可得使函數f（x）=x²+ax+b²有零點的概率為$\frac{\frac{1}{2}×4×2}{4×4}$=$\frac{1}{4}$，故正確；
②在△ABC中，$\overrightarrow{AB}$•$\overrightarrow{AC}$＞0只能得到A為銳角，推不出“△ABC為銳角三角形”，故不正確；
③已知x＞-1，y＞0且滿足x+2y=1，則$\frac{1}{x+1}$+$\frac{2}{y}$=$\frac{1}{x+1}$+$\frac{4}{1-x}$（-1＜x＜1）
=$\frac{1}{2}$[（1+x）+（1-x）]（$\frac{1}{x+1}$+$\frac{4}{1-x}$）=$\frac{1}{2}$[1+4+$\frac{1-x}{1+x}$+$\frac{4（1+x）}{1-x}$]≥$\frac{1}{2}$[5+2$\sqrt{\frac{1-x}{1+x}•\frac{4（1+x）}{1-x}}$]=$\frac{9}{2}$，
當且僅當1-x=2（1+x），即x=-$\frac{1}{3}$時取得最小值為$\frac{9}{2}$．故正確；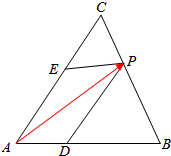
④在AB上取一點D，使得 $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$，在AC上取一點E，
使得：$\overrightarrow{AE}$=$\frac{2}{3}$$\overrightarrow{AC}$．
則由向量的加法的平行四邊形法則得：$\overrightarrow{AP}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$，
由圖可知，若點P落在△ABC的內部，則0＜t＜$\frac{2}{3}$．則④正確．
故答案為：①③④．

點評 本題考查命題的真假判斷和運用，主要考查幾何概率和充分必要條件的判斷，以及基本不等式的運用和平面向量定理的運用，屬于中檔題和易錯題．