
| 2 |
| 2 |
| a |
| 2 |
| -1-a2 |
| 2 |
| a |
| 2 |
| -1-a2 |
| 2 |
| (x1-x2)2+(x12-2ax1-x22+2ax2)2 |
| 1+a2 |
| (x1+x2)2-4x1x2 |
| 1+a2 |
| 2-a2 |
| 1+a2 |
| 2-a2 |
| 1 |
| 2 |
| ||
| 2 |


 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數系列答案
同步奧數系列答案科目:高中數學 來源: 題型:
 為考察中學生的性別與是否喜歡某項運動之間的關系,隨機抽取了某校的部分學生進行調查,并將調查數據制作成二維條形圖(如圖),若已知共有83名學生喜歡此項運動,且男生的喜歡比例比女生多29%,則女生中喜歡此項運動的比例是( )
為考察中學生的性別與是否喜歡某項運動之間的關系,隨機抽取了某校的部分學生進行調查,并將調查數據制作成二維條形圖(如圖),若已知共有83名學生喜歡此項運動,且男生的喜歡比例比女生多29%,則女生中喜歡此項運動的比例是( )| A、35% | B、36% |
| C、64% | D、65% |
查看答案和解析>>
科目:高中數學 來源: 題型:
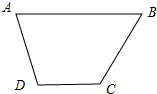 如圖,等腰梯形ABCD中,AB∥CD,且AB=2,AD=1,DC=2x(x∈(0,1)),以A,B為焦點,且過點D的雙曲線的離心率為e1.以C,D為焦點,且過點A的橢圓的離心率為e1,動點E在邊AB上,且|AE|<e1+e2,對x∈(0,1)恒成立,則|AE|的最大值為( )
如圖,等腰梯形ABCD中,AB∥CD,且AB=2,AD=1,DC=2x(x∈(0,1)),以A,B為焦點,且過點D的雙曲線的離心率為e1.以C,D為焦點,且過點A的橢圓的離心率為e1,動點E在邊AB上,且|AE|<e1+e2,對x∈(0,1)恒成立,則|AE|的最大值為( )A、
| ||
| B、2 | ||
C、
| ||
| D、不存在 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com