
分析 根據(jù)正方體和球的結(jié)構(gòu)特征,求得球O被平面ACD1所截得的圓的半徑r,再通過利用球的性質(zhì)求出O到平面ACD1的距離d,進而求出圓錐的高,再由勾股定理求出圓錐的母線,最后利用圓錐的表面積求解即可.
解答 解:如圖,O為球心,也是正方體的中心,
設球O被平面ACD1所截得的圓的半徑為r,AC中點為M,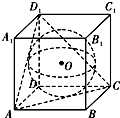
則r=$\frac{1}{3}$D1M=$\frac{\sqrt{6}}{6}$,
球的半徑R=$\frac{1}{2}$,
則O到平面ACD1的距離d=$\sqrt{{R}^{2}-{r}^{2}}$=$\frac{\sqrt{3}}{6}$,
則圓錐的高h=$\frac{\sqrt{3}}{6}+\frac{\sqrt{3}}{2}$=$\frac{2\sqrt{3}}{3}$,
故圓錐的母線長l=$\frac{\sqrt{6}}{2}$
故圓錐的表面積為:πr(r+h)=$\frac{\sqrt{6}}{6}$($\frac{\sqrt{6}}{6}+\frac{\sqrt{6}}{2}$)π=$\frac{2π}{3}$,
故答案為:$\frac{2π}{3}$.
點評 本題考查了正方體和它的內(nèi)接球的結(jié)構(gòu)特征、圓錐的體積,關鍵是想象出截面圖的形狀,考查了空間想象能力.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
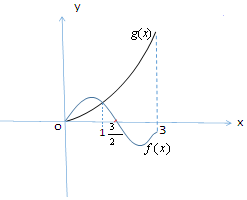 已知函數(shù)y=f(x)是偶函數(shù),y=g(x)是奇函數(shù),它們的定義域是[-3,3],它們在x∈[0,3]上的圖象如圖所示,則不等式f(x)•g(x)≥0的解集是[-3,-$\frac{3}{2}$]∪[0,$\frac{3}{2}$].
已知函數(shù)y=f(x)是偶函數(shù),y=g(x)是奇函數(shù),它們的定義域是[-3,3],它們在x∈[0,3]上的圖象如圖所示,則不等式f(x)•g(x)≥0的解集是[-3,-$\frac{3}{2}$]∪[0,$\frac{3}{2}$].查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com