Question

17．已知拋物線C：x²=2py（p＞0），P，Q是C上任意兩點，點M（0，-1）滿足$\overrightarrow{MP}•\overrightarrow{MQ}≥0$，則p的取值范圍是（0，2]．

Answer 1

分析 過G作拋物線的切線，根據導數的幾何意義，求得k=±$\sqrt{\frac{2}{p}}$，只需令切線的夾角小于90°即可，則$\sqrt{\frac{2}{p}}$≥1，即可求得p的取值范圍．

解答 解：過G點作拋物線的兩條切線，設切線方程為y=kx-1，
切點坐標為M（x₀，y₀），N（-x₀，y₀），
由y=$\frac{{x}^{2}}{2p}$，y′=$\frac{1}{p}$x，
則由導數的幾何意義可知$\left\{\begin{array}{l}{{x}_{0}^{2}={2py}_{0}}\\{{y}_{0}=k{x}_{0}-1}\\{\frac{{x}_{0}}{p}=k}\end{array}\right.$，解得k=±$\sqrt{\frac{2}{p}}$．
$\overrightarrow{MP}•\overrightarrow{MQ}≥0$恒成立，∠AOB≤90°，即∠AGO≤45°，
∴|k|＞tan45°=1，即$\sqrt{\frac{2}{p}}$≥1，
解得p≤2，
由p＞0，則0＜p≤2，
p的取值范圍：（0，2]，
故答案為：（0，2]．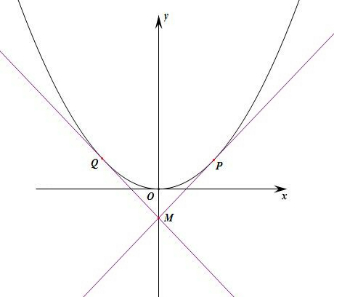

點評 本題考查了直線與拋物線的位置關系，導數的幾何意義，考查的數量積，考查數形結合思想，屬于中檔題．