
| A. | $\frac{{9\sqrt{3}}}{2}$ | B. | $\frac{8}{3}$ | C. | $\frac{26}{9}$ | D. | 3 |
分析 用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AE},\overrightarrow{AF}$,得出$\overrightarrow{AE}•\overrightarrow{AF}$關于bc的函數,利用基本不等式得出最小值.
解答 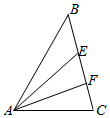 解:$\overrightarrow{AE}$=$\frac{2}{3}\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$,$\overrightarrow{AF}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$,
解:$\overrightarrow{AE}$=$\frac{2}{3}\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$,$\overrightarrow{AF}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$,
∴$\overrightarrow{AE}•\overrightarrow{AF}$=$\frac{2}{9}{\overrightarrow{AB}}^{2}$+$\frac{2}{9}$${\overrightarrow{AC}}^{2}$+$\frac{5}{9}$$\overrightarrow{AB}•\overrightarrow{AC}$,
∵b+c=4,
∴b2+c2=16-2bc,$\frac{2}{9}{\overrightarrow{AB}}^{2}$+$\frac{2}{9}$${\overrightarrow{AC}}^{2}$=$\frac{2}{9}$(16-2bc),$\frac{5}{9}$$\overrightarrow{AB}•\overrightarrow{AC}$=$\frac{5}{9}$bccosA=$\frac{5}{18}$bc,
∴$\overrightarrow{AE}•\overrightarrow{AF}$=$\frac{2}{9}$(16-2bc)+$\frac{5bc}{18}$=$\frac{32}{9}$-$\frac{3}{18}$bc,
∵bc≤($\frac{b+c}{2}$)2=4,
∴當bc=4時,$\overrightarrow{AE}•\overrightarrow{AF}$取得最小值$\frac{32}{9}-\frac{3}{18}×4$=$\frac{26}{9}$.
故選:C.
點評 本題考查了平面向量的數量積運算,基本不等式的應用,屬于中檔題.


科目:高中數學 來源: 題型:解答題
 已知球內接四棱錐P-ABCD的高為3,AC,BC相交于O,球的表面積為$\frac{169π}{9}$,若E為PC中點.
已知球內接四棱錐P-ABCD的高為3,AC,BC相交于O,球的表面積為$\frac{169π}{9}$,若E為PC中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
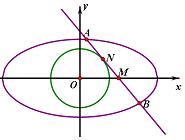 已知橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦點$(\sqrt{3},0)$,且經過點$(-1,\frac{{\sqrt{3}}}{2})$,點M是x軸上的一點,過點M的直線l與橢圓C交于A,B兩點(點A在x軸的上方)
已知橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦點$(\sqrt{3},0)$,且經過點$(-1,\frac{{\sqrt{3}}}{2})$,點M是x軸上的一點,過點M的直線l與橢圓C交于A,B兩點(點A在x軸的上方)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在菱形ABCD中,∠ABC=60°,AC與BD相交于點O,AE⊥平面ABCD,CF∥AE,AB=AE=2.
如圖,在菱形ABCD中,∠ABC=60°,AC與BD相交于點O,AE⊥平面ABCD,CF∥AE,AB=AE=2.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | 0 | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 0或$\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com