
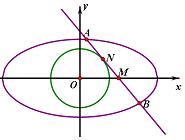
 已知橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦點(diǎn)$(\sqrt{3},0)$,且經(jīng)過(guò)點(diǎn)$(-1,\frac{{\sqrt{3}}}{2})$,點(diǎn)M是x軸上的一點(diǎn),過(guò)點(diǎn)M的直線(xiàn)l與橢圓C交于A,B兩點(diǎn)(點(diǎn)A在x軸的上方)
已知橢圓$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦點(diǎn)$(\sqrt{3},0)$,且經(jīng)過(guò)點(diǎn)$(-1,\frac{{\sqrt{3}}}{2})$,點(diǎn)M是x軸上的一點(diǎn),過(guò)點(diǎn)M的直線(xiàn)l與橢圓C交于A,B兩點(diǎn)(點(diǎn)A在x軸的上方)分析 (1)由題意列關(guān)于a,b的方程組,求解方程組可得a,b的值,則橢圓方程可求;
(2)設(shè)出M,A,B的坐標(biāo)及直線(xiàn)l的方程x=ty+m,與橢圓方程聯(lián)立,化為關(guān)于y的一元二次方程,由|AM|=2|MB|,有y1=-2y2,再結(jié)合根與系數(shù)的關(guān)系可得m與t的關(guān)系,由直線(xiàn)與圓相切可得m與t的另一關(guān)系式,聯(lián)立求得m,t的值,可得M的坐標(biāo),則|MN|的長(zhǎng)可求.
解答 解:(1)由題意知:$\left\{\begin{array}{l}{a^2}-{b^2}={c^2}=3\\ \frac{{{{(-1)}^2}}}{4}+\frac{{{{(-\frac{{\sqrt{3}}}{2})}^2}}}{b^2}=1\end{array}\right.$,
a2=3+b2>3,解得:a2=4,b2=1,
故橢圓C的方程為$\frac{x^2}{4}+{y^2}=1$;
(2)設(shè)M(m,0),直線(xiàn)l:x=ty+m,A(x1,y1),B(x2,y2),
由|AM|=2|MB|,有y1=-2y2,
由$\left\{\begin{array}{l}{x=ty+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得(t2+4)y2+2my+m2-4=0,
由韋達(dá)定理得:${y_1}+{y_2}=-\frac{2tm}{{{t^2}+4}},{y_1}{y_2}=\frac{{{m^2}-4}}{{{t^2}+4}}$,
由${y_1}{y_2}=-2y_2^2,{y_1}+{y_2}=-2{y_2}+{y_2}=-{y_2}$,
得${y_1}{y_2}=-2{[-({y_1}+{y_2})]^2}=-{({y_1}+{y_2})^2}$,即$\frac{{{m^2}-4}}{{{t^2}+4}},=-2{(-\frac{2tm}{{{t^2}+4}})^2}$,
化簡(jiǎn)得(m2-4)(t2+4)=-8t2m2,①
原點(diǎn)O到直線(xiàn)的距離$d=\frac{|m|}{{\sqrt{1+{t^2}}}}$,
又直線(xiàn)l與圓$O:{x^2}+{y^2}=\frac{4}{7}$相切,
∴$\frac{|m|}{{\sqrt{1+{t^2}}}}=\sqrt{\frac{4}{7}}$,即${t^2}=\frac{7}{4}{m^2}-1$,②
聯(lián)立①②得:21m4-16m2-16=0,即(3m2-4)(7m2+4)=0,
解得${m^2}=\frac{4}{3}$,此時(shí)${t^2}=\frac{4}{3}$,滿(mǎn)足△>0,得$M(±\frac{{2\sqrt{3}}}{3},0)$,
在Rt△OMN中,可得$|{MN}|=\sqrt{\frac{4}{3}-\frac{4}{7}}=\frac{{4\sqrt{21}}}{21}$,
∴|MN|的長(zhǎng)為$\frac{{4\sqrt{21}}}{21}$.
點(diǎn)評(píng) 本題考查橢圓的簡(jiǎn)單性質(zhì),考查了直線(xiàn)與圓、橢圓位置關(guān)系的應(yīng)用,體現(xiàn)了“設(shè)而不求”的解題思想方法,考查計(jì)算能力,是中檔題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
| 專(zhuān)業(yè)課成績(jī)xi(分) | 7 | 7 | 8 | 9 | 9 |
| 年薪y(tǒng)i(萬(wàn)元) | 10 | 12 | 14 | 14 | 15 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 5i | B. | -5i | C. | 5 | D. | -5 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\frac{{9\sqrt{3}}}{2}$ | B. | $\frac{8}{3}$ | C. | $\frac{26}{9}$ | D. | 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖,正方體ABCD-A1B1C1D1中,E,F(xiàn),M,N分別是A1B1,BC,C1D1,B1C1的中點(diǎn),求二面角M-EF-N的平面角的余弦值.
如圖,正方體ABCD-A1B1C1D1中,E,F(xiàn),M,N分別是A1B1,BC,C1D1,B1C1的中點(diǎn),求二面角M-EF-N的平面角的余弦值.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | ①④ | B. | ②④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com