
分析 (1)由條件,曲線在(0,f(0))處的切線斜率k=0,即f'(0)=1+a=0,可得a=-1,f'(x)=ex-1,再通過解不等式即可求出單調區間;
(2)利用轉化思想,x>0時,不等式(m-x)ex<m+2等價于$m<\frac{{x{e^x}+2}}{{{e^x}-1}}$,然后構造新函數,記g(x)=$\frac{x{e}^{x}+2}{{e}^{x}-1}$,根據(1)的結論可得存在x0∈(1,2),使得g'(x0)=0,且g(x)min=g(x0),再通過化簡運算可得g(x)min=x0+1,由x0∈(1,2),即可求出[m]的最大值.
解答 解:(1)函數f(x)的定義域為(-∞,+∞),f'(x)=ex+a,
由條件,f'(0)=1+a=0,得a=-1,則f'(x)=ex-1
由f'(x)=ex-1>0得x>0,由f'(x)<0得x<0,
故函數f(x)的單調遞增區間為(0,+∞),單調遞減區間為(-∞,0).
(2)x>0時,不等式(m-x)ex<m+2等價于$m<\frac{{x{e^x}+2}}{{{e^x}-1}}$,
令$g(x)=\frac{{x{e^x}+2}}{{{e^x}-1}}$,∴$g'(x)=\frac{{{e^x}({{e^x}-x-3})}}{{{{({{e^x}-1})}^2}}}$,
由(1)得u(x)=ex-x-3在(0,+∞)上單調遞增,
又∵u(1)<0,u(2)>0,
∴g'(x)在(0,+∞)上有唯一零點x0,且1<x0<2,
∴當x∈(1,x0)時,g'(x)<0,當x∈(x0+∞)時,g'(x)>0,
∴g(x)min=g(x0),由g'(x0)=0得${e^{x_0}}={x_0}+3$,
∴g(x)min=$g({x_0})=\frac{{{x_0}({{x_0}+3})+2}}{{{x_0}+2}}={x_0}+1$,
∵1<x0<2,∴2<g(x0)<3,
∵m<g(x0),∴[m]的最大值為2.
點評 本題考查了利用導數求切線的斜率和函數的單調區間,以及函數恒成立問題,著重考查了數學轉化思想方法,以及函數最值的求法,利用參數分離法是解決本題的關鍵.綜合性較強,難度較大.


科目:高中數學 來源: 題型:選擇題
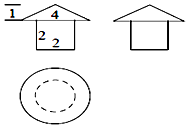
| A. | (6+2$\sqrt{5}$)π | B. | (8+2$\sqrt{5}$)π | C. | (9+2$\sqrt{5}$)π | D. | (10+2$\sqrt{5}$)π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 飛機的航線和山頂在同一個鉛垂直平面內,已知飛機的高度為海拔15000m,速度為1000km/h,飛行員先看到山頂的俯角為18°,經過108s后又看到山頂的俯角為78°,則山頂的海拔高度為( )
飛機的航線和山頂在同一個鉛垂直平面內,已知飛機的高度為海拔15000m,速度為1000km/h,飛行員先看到山頂的俯角為18°,經過108s后又看到山頂的俯角為78°,則山頂的海拔高度為( )| A. | (15-18$\sqrt{3}$sin18°cos78°)km | B. | (15-18$\sqrt{3}$sin18°sin78°)km | ||
| C. | (15-20$\sqrt{3}$sin18°cos78°)km | D. | (15-20$\sqrt{3}$sin18°sin78°)km |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-24,0) | B. | (-∞,-24)∪[0,2) | C. | (-24,3) | D. | (-∞,-24]∪[0,2] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,0) | B. | (-∞,2) | C. | (2,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com