
分析 (I)可假設存在實數a,b,使得y=f(x)的定義域和值域都是[a,b],由此出發探究a,b的可能取值,可分三類:a,b∈(0,$\frac{1}{2}$)時,a,b∈($\frac{1}{2}$,+∞)時,a∈(0,$\frac{1}{2}$),b∈($\frac{1}{2}$,+∞),分別建立方程,尋求a,b的可能取值,若能求出這樣的實數,則說明存在,否則說明不存在;
(II)由題意,由函數y=f (x)的定義域為[a,b],值域為[ma,mb](m≠0)可判斷出m>0及a>0,結合(I)的結論知只能a,b∈($\frac{1}{2}$,+∞),由函數在此區間內是增函數,建立方程,即可得到實數m所滿足的不等式,解出實數m的取值范圍.
解答 解:(I)不存在實數a,b滿足條件.
假設存在實數a,b,使得y=f(x)的定義域和值域都是[a,b],
而y≥0,x≠0,所以應有a>0,
又f(x)=$\left\{\begin{array}{l}{2-\frac{1}{x},x≥\frac{1}{2}}\\{\frac{1}{x}-2,0<x<\frac{1}{2}}\end{array}\right.$
(1)當a,b∈(0,$\frac{1}{2}$)時,f(x)=$\frac{1}{x}$-2在(0,$\frac{1}{2}$)上為減函數,
故有 $\left\{\begin{array}{l}{f(a)=b}\\{f(b)=a}\end{array}\right.$,即 $\left\{\begin{array}{l}{\frac{1}{a}-2=b}\\{\frac{1}{b}-2=a}\end{array}\right.$,由此可得a=b,此時實數a,b的值不存在.
(2)當a,b∈[$\frac{1}{2}$,+∞)時,f(x)=2-$\frac{1}{x}$在∈($\frac{1}{2}$,+∞)上為增函數,
故有 $\left\{\begin{array}{l}{f(a)=a}\\{f(b)=b}\end{array}\right.$,即$\left\{\begin{array}{l}{2-\frac{1}{a}=a}\\{2-\frac{1}{b}=b}\end{array}\right.$由此可得a,b是方程x2-2x+1=0的根,但方程有兩個相等實根,所以此時不成立.
(3)當a∈(0,$\frac{1}{2}$),b∈($\frac{1}{2}$,+∞)時,顯然$\frac{1}{2}$∈[a,b],而f($\frac{1}{2}$)=0∈[a,b]不可能,
此時a,b也不存在;
綜上可知,適合條件的實數a,b不存在.
(II)若存在實數a,b使函數y=f(x)的定義域為[a,b],值域為[ma,mb](m≠0).
由mb>ma,b>a得m>0,而ma>0,所以a>0
由(I)知a,b∈(0,$\frac{1}{2}$)或a∈(0,$\frac{1}{2}$),b∈($\frac{1}{2}$,+∞)時,適合條件的實數a,b不存在,
故只能是a,b∈($\frac{1}{2}$,+∞)
∵f(x)=2-$\frac{1}{x}$在∈($\frac{1}{2}$,+∞)上為增函數,
∴$\left\{\begin{array}{l}{f(a)=ma}\\{f(b)=mb}\end{array}\right.$,即$\left\{\begin{array}{l}{2-\frac{1}{a}=ma}\\{2-\frac{1}{b}=mb}\end{array}\right.$∴a,b是方程mx2-2x+1=0的兩個不等實根,
且二實根均大于$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{△=4-4m>0}\\{\frac{1}{4}m-1+1>0}\\{\frac{1}{m}>\frac{1}{2}}\end{array}\right.$,解之得0<m<1,
故實數m的取值范圍是(0,1).
點評 本題的考點是函數與方程的綜合應用,考察了絕對值函數,函數的定義域、值域構造方程的思想,二次方程根與系數的關系等,解題的關鍵是理解題意,將問題正確轉化,進行分類討論探究,本題考察了分類討論的思想,方程的思想,考察了推理判斷能力,是一道綜合性較強的題,思維難度大,解題時要嚴謹,本題易因為考慮不完善出錯.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|-3<x<0} | B. | {x|-1<x<0} | C. | {x|0<x<1} | D. | {x|0<x<3} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
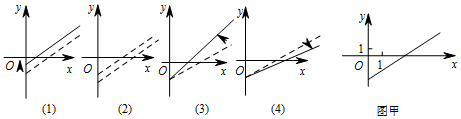
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com