
分析 (Ⅰ)利用橢圓經過的點,求出b,利用橢圓的離心率求解,a,b,得到橢圓方程.
(Ⅱ)設PA、PB的斜率分別為k1,k2,P(x0,y0),求出斜率的表達式,利用斜率乘積推出定值.得到MN的中點G(4,3k1+k2).寫出以MN為直徑的圓的方程,通過令y=0,求解存在定點(1,0),(7,0)經過以MN為直徑的圓.
解答  解:(Ⅰ)設Q(x0,4),代入y2=2px,得x0=$\frac{8}{p}$,$\frac{5}{4}$|RQ|=$\frac{8}{p}$,
解:(Ⅰ)設Q(x0,4),代入y2=2px,得x0=$\frac{8}{p}$,$\frac{5}{4}$|RQ|=$\frac{8}{p}$,
又丨QF丨=丨QF丨+$\frac{p}{2}$=|=$\frac{5}{4}$|RQ|,即$\frac{8}{p}$+$\frac{p}{2}$=$\frac{5}{4}$×$\frac{8}{p}$,解得:p=2.
∴拋物線C的標準方程為y2=4x.在橢圓E中,c=1,$\frac{c}{a}$=$\frac{1}{2}$,
∴a=2,b2=a2-c2=3.
∴橢圓E的標準方程為$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)設PA、PB的斜率分別為k1,k2,P(x0,y0),
取k1=$\frac{{y}_{0}}{{x}_{0}+2}$,k2=$\frac{{y}_{0}}{{x}_{0}-2}$,
則k1k2=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-4}$=$\frac{3(1-\frac{{x}_{0}^{2}}{4})}{{x}_{0}^{2}-4}$=$\frac{3×\frac{4-{x}_{0}^{2}}{4}}{{x}_{0}^{2}-4}$=-$\frac{3}{4}$,…(7分)
由lPA:y=k1(x+2)知M(4,6k1),由lPB:y=k2(x-2)知N(4,2k2),
∴MN的中點G(4,3k1+k2).
∴以MN為直徑的圓的方程為(x-4)2+(y-3k1-k2)2=$\frac{1}{4}$(6k1-2k2)2=(3k1-k2)2,
令y=0,∴x2-8x+16+9k12+6k1k2+k22=9k1-6k1k2+k22,
∴x2-8x+16+12k1k2=0,∴x2-8x+16+12×(-$\frac{3}{4}$)=0,
即x2-8x+7=0,解得x=7或x=1.
∴以MN為直徑的圓過定點(1,0),(7,0).
點評 本題考查橢圓的方程的求法,直線與橢圓的位置關系的綜合應用,圓的方程的應用,考查轉化思想以及計算能力,屬于中檔題.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:填空題
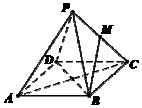 如圖,已知正四棱錐P-ABCD中,AB=4,高$h=2\sqrt{2}$,點M是側棱PC的中點,則異面直線BM與AC所成角的余弦值為$\frac{\sqrt{6}}{6}$.
如圖,已知正四棱錐P-ABCD中,AB=4,高$h=2\sqrt{2}$,點M是側棱PC的中點,則異面直線BM與AC所成角的余弦值為$\frac{\sqrt{6}}{6}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $3021+\sqrt{3}$ | B. | $3024+\sqrt{3}$ | C. | $3021+\frac{{\sqrt{3}-1}}{2}$ | D. | $3024+\frac{{\sqrt{3}-1}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?x0∈R,使得${e^{x_0}}≤0$ | |
| B. | $sinx+\frac{1}{sinx}≥2(x≠kπ,k∈Z)$ | |
| C. | ?x∈R,2x>x2 | |
| D. | 若命題p:?x0∈R,使得$x_0^2-{x_0}+1<0$,則¬p:?x0∈R,都有x2-x+1≥0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com