
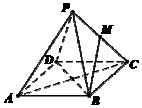
 如圖,已知正四棱錐P-ABCD中,AB=4,高$h=2\sqrt{2}$,點M是側棱PC的中點,則異面直線BM與AC所成角的余弦值為$\frac{\sqrt{6}}{6}$.
如圖,已知正四棱錐P-ABCD中,AB=4,高$h=2\sqrt{2}$,點M是側棱PC的中點,則異面直線BM與AC所成角的余弦值為$\frac{\sqrt{6}}{6}$. 分析 以O為原點,OA為x軸,OB為y軸,OP為z軸,建立空間直角坐標系,利用向量法能求出異面直線BM與AC所成角的余弦值.
解答 解:如圖,以O為原點,OA為x軸,OB為y軸,OP為z軸,建立空間直角坐標系,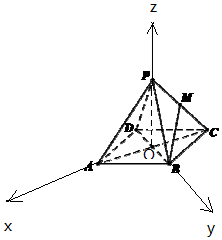
B(0,2$\sqrt{2}$,0),A(2$\sqrt{2}$,0,0),C(-2$\sqrt{2}$,0,0),
P(0,0,2$\sqrt{2}$),M(-$\sqrt{2}$,0,$\sqrt{2}$),
$\overrightarrow{BM}$=(-$\sqrt{2}$,-2$\sqrt{2}$,$\sqrt{2}$),$\overrightarrow{AC}$=(-4$\sqrt{2}$,0,0),
設異面直線BM與AC所成角為θ,
則cosθ=$\frac{|\overrightarrow{BM}•\overrightarrow{AC}|}{|\overrightarrow{BM}|•|\overrightarrow{AC}|}$=$\frac{8}{\sqrt{12}•4\sqrt{2}}$=$\frac{\sqrt{6}}{6}$.
∴異面直線BM與AC所成角的余弦值為$\frac{\sqrt{6}}{6}$.
故答案為:$\frac{{\sqrt{6}}}{6}$.
點評 本題考查異面直線所成角的余弦值的求法,是基礎題,解題時要認真審題,注意空間中線線、線面、面面間的位置關系的合理運用.


 每課必練系列答案
每課必練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 必要非充分條件 | B. | 充分非必要條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p∧q | B. | p∨q | C. | (¬p)∧(¬q) | D. | (¬p)∨q |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com