
分析 設圓臺的母線長為l,圓臺的底面面積為S=S上+S下=20π,圓臺的側面積S側=π(2+4)l=6πl,由此能求出該圓臺的母線長和體積.
解答 解:設圓臺的母線長為l,
則圓臺的上底面面積為S上=π•22=4π,
圓臺的下底面面積為S下=π•42=16π,
所以圓臺的底面面積為S=S上+S下=20π,
又圓臺的側面積S側=π(2+4)l=6πl,
于是6πl=20π,解得$l=\frac{10}{3}$,
∴圓臺高h=$\sqrt{{l}^{2}-(R-r{)^{2}}_{\;}^{\;}}$=$\sqrt{\frac{100}{9}-4}$=$\frac{8}{3}$,
∴圓臺體積V=$\frac{1}{3}π•h•({R}^{2}+{r}^{2}+Rr)$=$\frac{1}{3}π×\frac{8}{3}×(16+4+8)$=$\frac{224π}{9}$.
點評 本題考查圓臺的母線長和體積的求法,查數形結合和分類與整合的思想,考查學生分析問題和處理問題的能力.是中檔題.


科目:高中數學 來源: 題型:選擇題
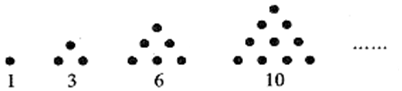
| A. | 45 | B. | 55 | C. | 65 | D. | 66 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
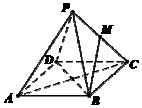 如圖,已知正四棱錐P-ABCD中,AB=4,高$h=2\sqrt{2}$,點M是側棱PC的中點,則異面直線BM與AC所成角的余弦值為$\frac{\sqrt{6}}{6}$.
如圖,已知正四棱錐P-ABCD中,AB=4,高$h=2\sqrt{2}$,點M是側棱PC的中點,則異面直線BM與AC所成角的余弦值為$\frac{\sqrt{6}}{6}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
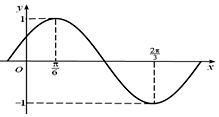 函數f(x)=Asin(ωx+φ)$({A>0,ω>0,|φ|<\frac{π}{2}})$的部分圖象如圖所示.
函數f(x)=Asin(ωx+φ)$({A>0,ω>0,|φ|<\frac{π}{2}})$的部分圖象如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $3021+\sqrt{3}$ | B. | $3024+\sqrt{3}$ | C. | $3021+\frac{{\sqrt{3}-1}}{2}$ | D. | $3024+\frac{{\sqrt{3}-1}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com