
分析 把an=Sn-Sn-1代入${S_n}^2-{a_n}{S_n}=2{a_n}$化簡即可得出{$\frac{2}{{S}_{n}}$}是等差數列,從而求出Sn,再利用an=Sn-Sn-1(n≥2)求出an即可.
解答 解:∵${S_n}^2-{a_n}{S_n}=2{a_n}$,
∴Sn2=2an+anSn=an(2+Sn)=(Sn-Sn-1)(2+Sn)=Sn2+2Sn-2Sn-1-SnSn-1,
∴2Sn-2Sn-1-SnSn-1=0,
∴$\frac{2}{{S}_{n-1}}-\frac{2}{{S}_{n}}-1=0$,即$\frac{2}{{S}_{n}}-\frac{2}{{S}_{n-1}}=-1$,
又$\frac{2}{{S}_{1}}$=-2,
∴{$\frac{2}{{S}_{n}}$}是以-2為首項,以-1為公差的等差數列,
∴$\frac{2}{{S}_{n}}$=-2-(n-1)=-n-1,
∴Sn=$\frac{-2}{n+1}$,
當n≥2時,an=Sn-Sn-1=$\frac{-2}{n+1}$+$\frac{2}{n}$=$\frac{2}{n(n+1)}$.
綜上,an=$\left\{\begin{array}{l}{-1,n=1}\\{\frac{2}{n(n+1)},n≥2}\end{array}\right.$.
故答案為:${a_n}=\left\{\begin{array}{l}-1,n=1\\ \frac{2}{n(n+1)},n≥2\end{array}\right.$;
點評 本題考查了等差關系的確定,數列通項公式的求法,屬于中檔題.


 互動英語系列答案
互動英語系列答案科目:高中數學 來源: 題型:選擇題
| A. | p∧q | B. | p∨q | C. | (¬p)∧(¬q) | D. | (¬p)∨q |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{15}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | M⊆N | B. | N⊆M | C. | ∁RN⊆M | D. | M⊆∁RN |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ($\sqrt{3}$,2$\sqrt{3}$) | B. | ($\sqrt{3}$,3$\sqrt{3}$) | C. | (3,$2\sqrt{3}$) | D. | (3,3$\sqrt{3}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
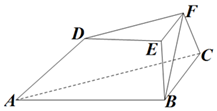 如圖,在三棱臺ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
如圖,在三棱臺ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com