
分析 (1)利用f(x)=2x-$\frac{a}{x}$,且f(2)=$\frac{9}{2}$,求實數a的值;
(2)利用奇偶函數的定義判斷該函數的奇偶性;
(3)判斷函數f(x)在(1,+∞)上的單調性,利用定義進行證明.
解答 解:(1)∵f(x)=2x-$\frac{a}{x}$,且f(2)=$\frac{9}{2}$,
∴4-$\frac{a}{2}$=$\frac{9}{2}$,
∴a=-1;(2分)
(2)由(1)得函數$f(x)=2x+\frac{1}{x}$,定義域為{x|x≠0}關于原點對稱…(3分)
∵$f(-x)=2(-x)+\frac{1}{-x}$=$-2x-\frac{1}{x}=-(2x+\frac{1}{x})=-f(x)$,
∴函數$f(x)=2x+\frac{1}{x}$為奇函數.…(6分)
(3)函數f(x)在(1,+∞)上是增函數,…(7分)
任取x1,x2∈(1,+∞),不妨設x1<x2,則$f({x_2})-f({x_1})=2{x_2}+\frac{1}{x_2}-(2{x_1}+\frac{1}{x_1})=2({x_2}-{x_1})+(\frac{1}{x_2}-\frac{1}{x_1})=2({x_2}-{x_1})+(\frac{{{x_1}-{x_2}}}{{{x_1}{x_2}}})$=$({x_2}-{x_1})(2-\frac{1}{{{x_1}{x_2}}})=\frac{{({x_2}-{x_1})(2{x_1}{x_2}-1)}}{{{x_1}{x_2}}}$…(10分)
∵x1,x2∈(1,+∞)且x1<x2∴x2-x1>0,2x1x2-1>0,x1x2>0
∴f(x2)-f(x1)>0,即f(x2)>f(x1),
∴f(x)在(1,+∞)上是增函數 …(12分)
點評 本題考查函數的單調性與奇偶性,考查學生分析解決問題的能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | $y=sin(2x-\frac{π}{6})$,x∈R | B. | $y=sin(\frac{x}{2}+\frac{π}{12})$,x∈R | C. | $y=sin(2x+\frac{π}{6})$,x∈R | D. | $y=sin(2x+\frac{π}{3})$,x∈R |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $0≤a≤\frac{1}{5}$ | B. | $a≤\frac{1}{5}$ | C. | a≥-3 | D. | $a≤\frac{1}{5}$或0 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
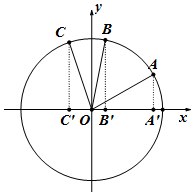 如圖,在平面直角坐標系中,銳角α、β及角α+β的終邊分別與單位圓O交于A,B,C三點.分別作AA'、BB'、CC'垂直于x軸,若以|AA'|、|BB'|、|CC'|為三邊長構造三角形,則此三角形的外接圓面積為( )
如圖,在平面直角坐標系中,銳角α、β及角α+β的終邊分別與單位圓O交于A,B,C三點.分別作AA'、BB'、CC'垂直于x軸,若以|AA'|、|BB'|、|CC'|為三邊長構造三角形,則此三角形的外接圓面積為( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{45}{4}$ | B. | 6 | C. | $\frac{45}{8}$ | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com