
【題目】如圖,AB是圓O的直徑,點C是圓O上異于A,B的點,直線PC⊥平面ABC,E,F分別是PA,PC的中點. 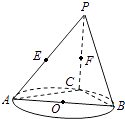
(1)記平面BEF與平面ABC的交線為l,試判斷直線l與平面PAC的位置關系,并加以證明;
(2)設(1)中的直線l與圓O的另一個交點為D,且點Q滿足 ![]() .記直線PQ與平面ABC所成的角為θ,異面直線PQ與EF所成的角為α,二面角E﹣l﹣C的大小為β.求證:sinθ=sinαsinβ.
.記直線PQ與平面ABC所成的角為θ,異面直線PQ與EF所成的角為α,二面角E﹣l﹣C的大小為β.求證:sinθ=sinαsinβ.
【答案】
(1)解:直線l∥平面PAC,證明如下:
連接EF,因為E,F分別是PA,PC的中點,所以EF∥AC,
又EF平面ABC,且AC平面ABC,所以EF∥平面ABC.
而EF平面BEF,且平面BEF∩平面ABC=l,所以EF∥l.
因為l平面PAC,EF平面PAC,所以直線l∥平面PAC.
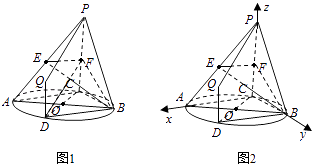
(2)解:(綜合法)如圖1,連接BD,由(1)可知交線l即為直線BD,且l∥AC.
因為AB是⊙O的直徑,所以AC⊥BC,于是l⊥BC.
已知PC⊥平面ABC,而l平面ABC,所以PC⊥l.
而PC∩BC=C,所以l⊥平面PBC.
連接BE,BF,因為BF平面PBC,所以l⊥BF.
故∠CBF就是二面角E﹣l﹣C的平面角,即∠CBF=β.
由 ![]() ,作DQ∥CP,且
,作DQ∥CP,且 ![]() .
.
連接PQ,DF,因為F是CP的中點,CP=2PF,所以DQ=PF,
從而四邊形DQPF是平行四邊形,PQ∥FD.
連接CD,因為PC⊥平面ABC,所以CD是FD在平面ABC內的射影,
故∠CDF就是直線PQ與平面ABC所成的角,即∠CDF=θ.
又BD⊥平面PBC,有BD⊥BF,知∠BDF=α,
于是在Rt△DCF,Rt△FBD,Rt△BCF中,分別可得 ![]() ,
,
從而 ![]() .
.
(向量法)如圖2,由 ![]() ,作DQ∥CP,且
,作DQ∥CP,且 ![]() .
.
連接PQ,EF,BE,BF,BD,由(Ⅰ)可知交線l即為直線BD.
以點C為原點,向量 ![]() 所在直線分別為x,y,z軸,建立如圖所示的空間直角坐標系,設CA=a,CB=b,CP=2c,則有
所在直線分別為x,y,z軸,建立如圖所示的空間直角坐標系,設CA=a,CB=b,CP=2c,則有 ![]() .
.
于是 ![]() ,
,
∴ 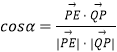 =
= ![]() ,從而
,從而 ![]() ,
,
又取平面ABC的一個法向量為 ![]() ,可得
,可得 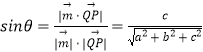 ,
,
設平面BEF的一個法向量為 ![]() ,
,
所以由 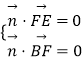 可得
可得 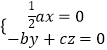 取
取 ![]() =(0,c,b),
=(0,c,b),
于是 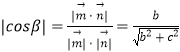 ,從而
,從而 ![]() .
.
故 ![]() ,即sinθ=sinαsinβ.
,即sinθ=sinαsinβ.
【解析】(1)直線l∥平面PAC.連接EF,利用三角形的中位線定理可得,EF∥AC;利用線面平行的判定定理即可得到EF∥平面ABC.由線面平行的性質定理可得EF∥l.再利用線面平行的判定定理即可證明直線l∥平面PAC.(2)綜合法:利用線面垂直的判定定理可證明l⊥平面PBC.連接BE,BF,因為BF平面PBC,所以l⊥BC.故∠CBF就是二面角E﹣l﹣C的平面角,即∠CBF=β.已知PC⊥平面ABC,可知CD是FD在平面ABC內的射影,故∠CDF就是直線PQ與平面ABC所成的角,即∠CDF=θ.由BD⊥平面PBC,有BD⊥BF,知∠BDF=α,分別利用三個直角三角形的邊角關系即可證明結論;
向量法:以點C為原點,向量 ![]() 所在直線分別為x,y,z軸,建立如圖所示的空間直角坐標系,利用兩個平面的法向量的夾角即可得出二面角.
所在直線分別為x,y,z軸,建立如圖所示的空間直角坐標系,利用兩個平面的法向量的夾角即可得出二面角.
【考點精析】解答此題的關鍵在于理解空間中直線與平面之間的位置關系的相關知識,掌握直線在平面內—有無數個公共點;直線與平面相交—有且只有一個公共點;直線在平面平行—沒有公共點,以及對直線與平面平行的判定的理解,了解平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行.


科目:高中數學 來源: 題型:
【題目】(2015·陜西)如圖,一橫截面為等腰梯形的水渠,因泥沙沉積,導致水渠截面邊界呈拋物線型(圖中虛線表示),則原始的最大流量與當前最大流量的比值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次馬拉松比賽中,35名運動員的成績(單位:分鐘)的莖葉圖如圖所示,若將運動員按成績由好到差編為![]() 號,再用系統抽樣方法從中抽取7人,則其中成績在區間
號,再用系統抽樣方法從中抽取7人,則其中成績在區間![]() 上的運動員人數是
上的運動員人數是 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·湖南)某工作的三視圖如圖3所示,現將該工作通過切削,加工成一個體積盡可能大的正方體新工件,并使新工件的一個面落在原工作的一個面內,則原工件材料的利用率為(材料利用率=新工件的體積/原工件的體積)
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了鼓勵市民節約用電,實行“階梯式”電價,將該市每戶居民的月用電量劃分為三檔,月用電量不超過200度的部分按0.5元/度收費,超過200度但不超過400度的部分按0.8元/度收費,超過400度的部分按1.0元/度收費.
(1)求某戶居民用電費用 ![]() (單位:元)關于月用電量
(單位:元)關于月用電量 ![]() (單位:度)的函數解析式;
(單位:度)的函數解析式;
(2)為了了解居民的用電情況,通過抽樣,獲得了今年1月份100戶居民每戶的用電量,統計分析后得到如圖所示的頻率分布直方圖,若這100戶居民中,今年1月份用電費用不超過260元的點80%,求 ![]() 的值;
的值;
(3)在滿足(2)的條件下,若以這100戶居民用電量的頻率代替該月全市居民用戶用電量的概率,且同組中的數據用該組區間的中點值代替,記 ![]() 為該居民用戶1月份的用電費用,求
為該居民用戶1月份的用電費用,求 ![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+a|+|x﹣2|
(1)當a=﹣3時,求不等式f(x)≥3的解集;
(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四邊形ABEF是正方形,且平面ABEF⊥平面ABCD,M為AF的中點, (I)求證:AC⊥BM;
(II)求異面直線CE與BM所成角的余弦值.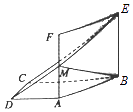
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com