
【題目】如圖所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四邊形ABEF是正方形,且平面ABEF⊥平面ABCD,M為AF的中點, (I)求證:AC⊥BM;
(II)求異面直線CE與BM所成角的余弦值.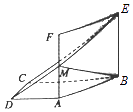
【答案】解:(I)證明:∵四邊形ABEF為正方形,∴BE⊥AB.
∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,BE平面ABEF.
∴BE⊥平面ABCD.
∵AC平面ABCD,∴BE⊥AC.
設AD=1,則 ![]() ,
,
∴AC⊥AB且AB∩BE=B,
∴AC⊥平面ABEF,又BM平面ABEF.∴AC⊥BM.
(II)取BC的中點記為Q,BE的中點記為N,連接MN,QN,DQ,
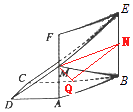
易得 ![]() .
.
在直角梯形ABCD中,由BC=2AD=2DC,
可得 ![]() ,
,
∴四邊形DMNQ為平行四邊形,
可得DM∥QN.
故DM∥CE,
那么∠DMB即為異面直線CE與BM所成的角(或其補角)
設BC=2a,則AD=DC=a,
可得 ![]() .
. 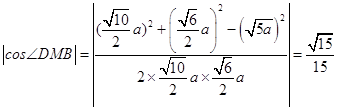 .
.
得異面直線CE與BM所成角的余弦值為 ![]() .
.
【解析】(I)線線垂直轉化為線面垂直,要證明AC⊥BM;只需證明BE⊥平面ABCD,即可.(II)取BC的中點記為Q,BE的中點記為N,連接MN,QN,DQ,易得 ![]() .在直角梯形ABCD中,由BC=2AD=2DC可得
.在直角梯形ABCD中,由BC=2AD=2DC可得 ![]() ,所以四邊形DMNQ為平行四邊形,可得DM∥QN.故DM∥CE,∠DMB即為異面直線CE與BM所成的角(或其補角),利用余弦定理求解即可.
,所以四邊形DMNQ為平行四邊形,可得DM∥QN.故DM∥CE,∠DMB即為異面直線CE與BM所成的角(或其補角),利用余弦定理求解即可.
【考點精析】本題主要考查了異面直線及其所成的角和直線與平面垂直的性質的相關知識點,需要掌握異面直線所成角的求法:1、平移法:在異面直線中的一條直線中選擇一特殊點,作另一條的平行線;2、補形法:把空間圖形補成熟悉的或完整的幾何體,如正方體、平行六面體、長方體等,其目的在于容易發現兩條異面直線間的關系;垂直于同一個平面的兩條直線平行才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】如圖,AB是圓O的直徑,點C是圓O上異于A,B的點,直線PC⊥平面ABC,E,F分別是PA,PC的中點. 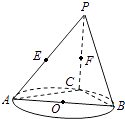
(1)記平面BEF與平面ABC的交線為l,試判斷直線l與平面PAC的位置關系,并加以證明;
(2)設(1)中的直線l與圓O的另一個交點為D,且點Q滿足 ![]() .記直線PQ與平面ABC所成的角為θ,異面直線PQ與EF所成的角為α,二面角E﹣l﹣C的大小為β.求證:sinθ=sinαsinβ.
.記直線PQ與平面ABC所成的角為θ,異面直線PQ與EF所成的角為α,二面角E﹣l﹣C的大小為β.求證:sinθ=sinαsinβ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,射線l:θ= ![]() 與圓C:ρ=2交于點A,橢圓Γ的方程為ρ2=
與圓C:ρ=2交于點A,橢圓Γ的方程為ρ2= ![]() ,以極點為原點,極軸為x軸正半軸建立平面直角坐標系xOy (Ⅰ)求點A的直角坐標和橢圓Γ的參數方程;
,以極點為原點,極軸為x軸正半軸建立平面直角坐標系xOy (Ⅰ)求點A的直角坐標和橢圓Γ的參數方程;
(Ⅱ)若E為橢圓Γ的下頂點,F為橢圓Γ上任意一點,求 ![]()
![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓W: ![]() (a>b>0)的上下頂點分別為A,B,且點B(0,﹣1).F1 , F2分別為橢圓W的左、右焦點,且∠F1BF2=120°.
(a>b>0)的上下頂點分別為A,B,且點B(0,﹣1).F1 , F2分別為橢圓W的左、右焦點,且∠F1BF2=120°.
(Ⅰ)求橢圓W的標準方程;
(Ⅱ)點M是橢圓上異于A,B的任意一點,過點M作MN⊥y軸于N,E為線段MN的中點.直線AE與直線y=﹣1交于點C,G為線段BC的中點,O為坐標原點.求∠OEG的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下莖葉圖記錄了甲、乙兩組各六名學生在一次數學測試中的成績(單位:分),規定85分以上(含85分)為優秀,現分別從甲、乙兩組中隨機選取一名同學的數學成績,則兩人成績都為優秀的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點F是拋物線τ:x2=2py (p>0)的焦點,點A是拋物線上的定點,且 ![]() =(2,0),點B,C是拋物線上的動點,直線AB,AC斜率分別為k1 , k2 .
=(2,0),點B,C是拋物線上的動點,直線AB,AC斜率分別為k1 , k2 . 
( I)求拋物線τ的方程;
(Ⅱ)若k1﹣k2=2,點D是點B,C處切線的交點,記△BCD的面積為S,證明S為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某理財公司有兩種理財產品A和B.這兩種理財產品一年后盈虧的情況如下(每種理財產品的不同投資結果之間相互獨立): 產品A產品B(其中p、q>0)
投資結果 | 獲利40% | 不賠不賺 | 虧損20% |
概率 |
|
|
|
投資結果 | 獲利20% | 不賠不賺 | 虧損10% |
概率 | p |
|
(1)已知甲、乙兩人分別選擇了產品A和產品B進行投資,如果一年后他們中至少有一人獲利的概率大于 ![]() ,求p的取值范圍;
,求p的取值范圍;
(2)丙要將家中閑置的10萬元錢進行投資,以一年后投資收益的期望值為決策依據,在產品A和產品B之中選其一,應選用哪個?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com