
分析 (Ⅰ)求出導數,討論導數的符號,確定其單調區間,從而確定極值.
(Ⅱ)g(x)定義域是(0,+∞),$g'(x)=x+\frac{1}{x}-2a$.分以下兩種情況討論,①若a≤1,②若a>1.
解答 解:(Ⅰ)f(x)定義域是(0,+∞),$f'(x)=\frac{{1-3{x^2}}}{x}$,令f'(x)=0得$x=\frac{{\sqrt{3}}}{3}$.
列表
| x | $(0,\frac{{\sqrt{3}}}{3})$ | $\frac{{\sqrt{3}}}{3}$ | (0,+∞) |
| f'(x) | + | 0 | - |
| f(x) | ↗ | $-\frac{1}{2}-\frac{1}{2}ln3$ | ↘ |
點評 本題考查了導數的綜合應用,利用導數求極值、最值,考查了計算能力,屬于壓軸題,


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | g(x)為奇函數 | B. | g(x)為偶函數 | ||
| C. | g(x)在$[0,\frac{π}{3}]$上單調遞增 | D. | g(x)的一個對稱中心為$(-\frac{π}{2},0)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
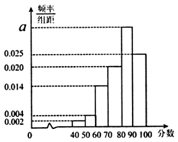 某地教育主管部門對所管轄的學校進行年終督導評估,為了解某學校師生對學校教學管理的滿意度,分別從教師和不同年級的學生中隨機抽取若干師生,進行評分(滿分100分),繪制如下頻率分布直方圖,并將分數從低到高分為四個等級:
某地教育主管部門對所管轄的學校進行年終督導評估,為了解某學校師生對學校教學管理的滿意度,分別從教師和不同年級的學生中隨機抽取若干師生,進行評分(滿分100分),繪制如下頻率分布直方圖,并將分數從低到高分為四個等級:| 滿意度評分 | 低于60分 | 60分到79分 | 80分到89分 | 90分及以上 |
| 滿意度等級 | 不滿意 | 基本滿意 | 滿意 | 非常滿意 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com