
分析 由f′(x)<2,則f(x)<2x+1可抽象出一個新函數g(x),利用新函數的性質(單調性)解決問題,即可得到答案.
解答 解:設g(x)=f(x)-(2x+1),
因為f(3)=7,f′(x)<2,
所以g(3)=f(3)-(2×3+1)=0,
g′(x)=f′(x)-2<0,
所以g(x)在R上是減函數,且g(3)=0.
所以f(x)<2x+1的解集即是g(x)<0=g(3)的解集.
所以x>3.
故答案為:(3,+∞).
點評 本題考查利用導數研究函數的單調性,解決此類問題的關鍵是構造函數g(x)=f(x)-(2x+1),然后利用導數研究g(x)的單調性,從而解決問題,屬于中檔題.


 習題精選系列答案
習題精選系列答案科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
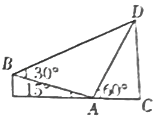 如圖所示,在直角梯形BECD中,A為線段CE上一點,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,則為CD=6$\sqrt{6}$m.
如圖所示,在直角梯形BECD中,A為線段CE上一點,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,則為CD=6$\sqrt{6}$m.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {3,4} | B. | {3,6} | C. | {1,3} | D. | {1,4} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
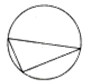 如圖,圓被其內接三角形分為4塊,現有5種顏色準備用來涂這4塊,要求每塊涂一種顏色,且相鄰兩塊的顏色不同,則不同的涂色方法有320種.(填數字)
如圖,圓被其內接三角形分為4塊,現有5種顏色準備用來涂這4塊,要求每塊涂一種顏色,且相鄰兩塊的顏色不同,則不同的涂色方法有320種.(填數字)查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com