
分析 (1)如果命題p為真命題,則f′(x)=3x2+2ax+1≥0對x∈(-∞,+∞)恒成立,進而得到實數a的取值范圍;
(2)如果命題“p∨q”為真命題,“p∧q”為假命題,則p,q一真一假,進而得到實數a的取值范圍.
解答 解:(1)如果命題p為真命題,
∵函數f(x)=x3+ax2+x在R上是增函數,
∴f′(x)=3x2+2ax+1≥0對x∈(-∞,+∞)恒成立…(3分)
∴$△=4{a^2}-12≤0⇒a∈[{-\sqrt{3},\sqrt{3}}]$…(6分)
(2)g′(x)=ex-1≥0對任意的x∈[0,+∞)恒成立,
∴g(x)在區間[0,+∞)遞增
命題q為真命題g(0)=a+1>0⇒a>-1…(9分)
由命題“p∨q”為真命題,“p∧q”為假命題知p,q一真一假,
若p真q假,則$\left\{\begin{array}{l}-\sqrt{3}≤a≤\sqrt{3}\\ a≤-1\end{array}\right.⇒a∈[{-\sqrt{3},-1}]$…(11分)
若p假q真,則$\left\{\begin{array}{l}a<-\sqrt{3}或a>\sqrt{3}\\ a>-1\end{array}\right.⇒a∈(\sqrt{3},+∞)$…(13分)
綜上所述,$a∈[{-\sqrt{3},-1}]∪(\sqrt{3},+∞)$…(14分)
點評 本題以命題的真假判斷與應用為載體,考查了導數法研究函數的單調性,復合命題,函數的零點,難度中檔.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:高中數學 來源: 題型:選擇題
| A. | ac>bc | B. | $\frac{b}{a}$>1 | C. | |a|>|b| | D. | ($\frac{1}{2}$)a<($\frac{1}{2}$)b |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
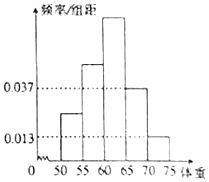 為了解今年某校高三畢業班想參軍的學生體重情況,將所得的數據整理后,畫出了頻率分布直方圖(如圖).已知圖中從左到右的前3個小組的頻率之比為1:2:3,其中第2小組的頻數為24.
為了解今年某校高三畢業班想參軍的學生體重情況,將所得的數據整理后,畫出了頻率分布直方圖(如圖).已知圖中從左到右的前3個小組的頻率之比為1:2:3,其中第2小組的頻數為24.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{49}{6}$ | B. | $\frac{25}{6}$ | C. | $\frac{8}{3}$ | D. | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com