
分析 設切點為(x0,x0lnx0),對y=xlnx求導數得y′=lnx+1,從而得到切線的斜率k=lnx0+1,結合直線方程的點斜式化簡得切線方程為y=(lnx0+1)x-x0,對照已知直線列出關于x0、m的方程組,解之即可得到實數m的值.
解答 解:設切點為(x0,x0lnx0),
對y=xlnx求導數,得y′=lnx+1,
∴切線的斜率k=lnx0+1,
故切線方程為y-x0lnx0=(lnx0+1)(x-x0),
整理得y=(lnx0+1)x-x0,
與y=2x+b比較得lnx0+1=2且-x0=b,
解得x0=e,故b=-e.
故b的值為:-e.
點評 本題考查導數的幾何意義,切線方程的求法,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
| 高一 | 高二 | 總計 | |
| 合格人數 | 70 | x | 150 |
| 不合格人數 | y | 20 | 50 |
| 總計 | 100 | 100 | 200 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 30o | B. | 60o | C. | 120o | D. | 150o |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
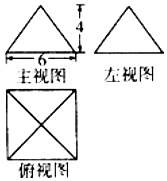 已知某幾何體的三視圖如圖所示,俯視圖是正方形,正視圖和側視圖都是底面邊長為6,高為4的等腰三角形.
已知某幾何體的三視圖如圖所示,俯視圖是正方形,正視圖和側視圖都是底面邊長為6,高為4的等腰三角形.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com