
分析 (Ⅰ)根據切線的斜率,求出b的值即可;
(Ⅱ)求出g(x)的導數,問題a≥$\frac{1}{x}$+ln x,令h(x)=$\frac{1}{x}$+ln x(x>0),根據函數的單調性求出a的范圍即可.
解答 解:(Ⅰ)由題意知,曲線y=f(x)在點(1,f(1))處的切線斜率為2,所以f′(1)=2,-------(2分)
又f′(x)=ln x+$\frac{b}{x}$+1,即ln 1+b+1=2,所以b=1.---------------------------------(4分)
(Ⅱ)由(Ⅰ)知 g(x)=${e^x}(\frac{f(x)}{x+1}-a)$=exln x-aex
所以 g′(x)=($\frac{1}{x}$-a+ln x)ex(x>0),----------------------------------------------------(6分)
若g(x)在(0,+∞)上為單調遞減函數,則g′(x)≤0在(0,+∞)上恒成立,
即$\frac{1}{x}$-a+ln x≤0,所以a≥$\frac{1}{x}$+ln x.-----------------------------------------------------(8分)
令h(x)=$\frac{1}{x}$+ln x(x>0),則h′(x)=-$\frac{1}{x2}$+$\frac{1}{x}$=$\frac{x-1}{x2}$
由h′(x)>0,得x>1,h′(x)<0,得0<x<1,
故函數h(x)在(0,1]上是減函數,在[1,+∞)上是增函數,
則$\frac{1}{x}$+ln x→∞,h(x)無最大值,g′(x)≤0在(0,+∞)上不恒成立,
故g(x)在(0,+∞)不可能是單調減函數.------------------------------------------------------(10分)
若g(x)在(0,+∞)上為單調遞增函數,則g′(x)≥0在(0,+∞)上恒成立,
即$\frac{1}{x}$-a+ln x≥0,所以a≤$\frac{1}{x}$+ln x,由前面推理知,h(x)=$\frac{1}{x}$+ln x的最小值為1,
∴a≤1,故a的取值范圍是(-∞,1].-------------------------------------------------------(12分)
點評 本題考查了函數的單調性、最值問題,考查導數的應用以及函數恒成立問題,是一道中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | $3\sqrt{2}$ | B. | 4 | C. | $\sqrt{34}$ | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
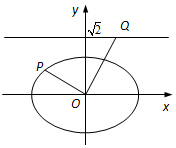 如圖,在平面直角坐標系xOy中,已知橢圓$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的離心率為$\frac{{\sqrt{2}}}{2}$,焦點到相應準線的距離為1.
如圖,在平面直角坐標系xOy中,已知橢圓$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的離心率為$\frac{{\sqrt{2}}}{2}$,焦點到相應準線的距離為1.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
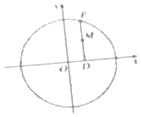 如圖,在圓x2+y2=9上任取一點P,過點P作x軸的垂線PD,D為垂足,點M滿足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;當點P在圓x2+y2=9上運動時,點M的軌跡為E.
如圖,在圓x2+y2=9上任取一點P,過點P作x軸的垂線PD,D為垂足,點M滿足$\overrightarrow{DM}=\frac{2}{3}\overrightarrow{DP}$;當點P在圓x2+y2=9上運動時,點M的軌跡為E.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 分組 | 頻數 | 頻率 |
| [50,60) | 5 | 0.05 |
| [60,70) | a | 0.20 |
| [70,80) | 35 | b |
| [80,90) | 25 | 0.25 |
| [90,100) | 15 | 0.15 |
| 合計 | 100 | 1.00 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com