Question

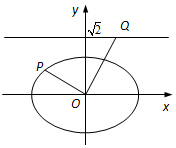
9．如圖，在平面直角坐標系xOy中，已知橢圓$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的離心率為$\frac{{\sqrt{2}}}{2}$，焦點到相應準線的距離為1．
（1）求橢圓的標準方程；
（2）若P為橢圓上的一點，過點O作OP的垂線交直線$y=\sqrt{2}$于點Q，求$\frac{1}{{O{P^2}}}+\frac{1}{{O{Q^2}}}$的值．

Answer 1

分析 （1）由已知條件可得$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$，$\frac{a^2}{c}-c=1$，然后求解橢圓的方程．
（2）由題意知OP的斜率存在．當OP的斜率為0時，求解結果；當OP的斜率不為0時，設直線OP方程為y=kx．聯立方程組，推出$O{P^2}=\frac{{2{k^2}+2}}{{2{k^2}+1}}$．OQ²=2k²+2．然后求解即可．

解答 解：（1）由題意得，$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$，$\frac{a^2}{c}-c=1$，…2分
解得$a=\sqrt{2}$，c=1，b=1．
所以橢圓的方程為$\frac{x^2}{2}+{y^2}=1$．  …4分
（2）由題意知OP的斜率存在．
當OP的斜率為0時，$OP=\sqrt{2}$，$OQ=\sqrt{2}$，所以$\frac{1}{{O{P^2}}}+\frac{1}{{O{Q^2}}}=1$．  …6分
當OP的斜率不為0時，設直線OP方程為y=kx．
由$\left\{\begin{array}{l}\frac{x^2}{2}+{y^2}=1\;\\ y=kx\;\end{array}\right.$得（2k²+1）x²=2，解得${x^2}=\frac{2}{{2{k^2}+1}}$，所以${y^2}=\frac{{2{k^2}}}{{2{k^2}+1}}$，
所以$O{P^2}=\frac{{2{k^2}+2}}{{2{k^2}+1}}$． …9分
因為OP⊥OQ，所以直線OQ的方程為$y=-\frac{1}{k}x$．
由$\left\{\begin{array}{l}y=\sqrt{2}\;\\ y=-\frac{1}{k}x\end{array}\right.$得$x=-\sqrt{2}k$，所以OQ²=2k²+2．  …12分
所以$\frac{1}{{O{P^2}}}+\frac{1}{{O{Q^2}}}=\frac{{2{k^2}+1}}{{2{k^2}+2}}+\frac{1}{{2{k^2}+2}}=1$．
綜上，可知$\frac{1}{{O{P^2}}}+\frac{1}{{O{Q^2}}}=1$．  …14分．

點評 本題考查橢圓的簡單性質的應用，直線與橢圓的位置關系的綜合應用，考查轉化思想以及計算能力．