考點:函數單調性的判斷與證明,函數奇偶性的判斷
專題:函數的性質及應用,導數的綜合應用
分析:(1)先求f(x)的定義域,知道定義域關于原點對稱,然后容易求得f(-x)=-f(x),所以得到函數f(x)為奇函數;
(2)可以用兩種方法討論f(x)的單調性:第一種方法,可以用導數法,求f′(x),通過解f′(x)≥0,f′(x)<0即可得到f(x)的單調區間,即判斷出f(x)的單調性;第二種方法,用單調性的定義,在定義域上任取x1,x2,且x1<x2,通過作差比較f(x1),f(x2)的大小,從而得出f(x)的單調區間,從而判斷出f(x)的單調性.
解答:
解:(1)f(x)的定義域為{x|x≠0};
f(-x)=-x-
=-f(x);
∴f(x)為奇函數;
(2)方法(一):
f′(x)=1
-=;
∴x
∈[-,0)或(0,]時,f′(x)≤0,∴f(x)在
[-,0),(0,]上單調遞減;
x
∈(-∞,-),或(,+∞)時,f′(x)>0,∴f(x)在(
-∞,-),
(,+∞)上單調遞增;
方法(二):
設x
1,x
2∈{x|x≠0},且x
1<x
2,則:
f(x
1)-f(x
2)=
x1-x2+-=(x1-x2)(1-)=
(x1x2-a);
∴①
x1,x2∈[-,0),或(0,]時,x
1x
2-a≤0,x
1x
2>0,x
1-x
2<0;
∴f(x
1)>f(x
2);
∴f(x)在
[-,0),(0,]上單調遞減;
②
x1,x2∈(-∞,-),或(,+∞)時,x
1x
2-a>0,x
1x
2>0,x
1-x
2<0;
∴f(x
1)<f(x
2);
∴f(x)在(-∞,-
),(
,+∞)上單調遞增.
點評:考查奇函數的定義,以及判斷一個函數奇偶性的過程,根據導數符號判斷函數單調性的方法,以及單調性的定義及利用定義判斷函數的單調性的過程.



 閱讀快車系列答案
閱讀快車系列答案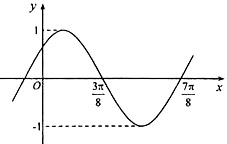 已知函數y=sin(ωx+φ)(ω>0,|φ|<
已知函數y=sin(ωx+φ)(ω>0,|φ|<