Question

5．隨著生活水平的提高，人們對空氣質量的要求越來越高，某機構為了解公眾對“車輛限行”的態度，隨機抽查40人，并將調查情況進行整理后制成如表：

年齡（歲）	[15，25）	[25，35）	[35，45）	[45，55）	[55，65）
頻數	5	10	10	5	10
贊成人數	4	6	8	4	9

（1）完成被調查人員年齡的頻率分布直方圖，并求被調査人員中持贊成態度人員的平均年齡約為多少歲？
（2）若從年齡在[15，25），[45，55）的被調查人員中各隨機選取1人進行調查．請寫出所有的基本亊件，并求選取2人中恰有1人持不贊成態度的概率．

Answer 1

分析 （1）由頻率數分布列能求出被調查人員年齡的頻率分布直方圖，由頻率分布直方圖能求出被調查人員持贊成態度人的平均年齡．
（2）設[15，25）中贊成的4人分別為A₁，A₂，A₃，A₄，不贊成的1人為a，[45，55）中贊成的4人分別為B₁，B₂，B₃，B₄，不贊成的1人為b．由此利用列舉法能求出恰有1人持不贊成態度的概率．

解答 解：（1）被調查人員年齡的頻率分布直方圖如圖所示：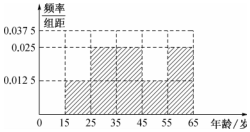

被調查人員持贊成態度人的平均年齡約為：
$\overline x=\frac{4×20+6×30+8×40+4×50+9×60}{4+6+8+4+9}≈42.6$（歲）．
（2）設[15，25）中贊成的4人分別為A₁，A₂，A₃，A₄，不贊成的1人為a，
[45，55）中贊成的4人分別為B₁，B₂，B₃，B₄，不贊成的1人為b．基本事件為：
（A₁，B₁），（A₁，B₂），（A₁，B₃），（A₁，B₄），（A₁，b），（A₂，B₁），
（A₂，B₂），（A₂，B₃），（A₂，B₄），（A₂，b），（A₃，B₁），（A₃，B₂），
（A₃，B₃），（A₃，B₄），（A₃，b），（A₄，B₁），（A₄，B₂），（A₄，B₃），
（A₄，B₄），（A₄，b），（a，B₁），（a，B₂），（a，B₃），（a，B₄），（a，b），
基本事件共有5×5=25個，
其中恰有1人持不贊成態度的基本事件為1+1+1+1+4=8個．
據古典概型知：恰有1人持不贊成態度的概率$P=\frac{8}{25}$．

點評 本題考查頻率分布直方圖的應用，考查概率的求法，是基礎題，解題時要認真審題，注意列舉法的合理運用．