
| A. | p1,p2,p3 | B. | p1,p2,p4 | C. | p1,p3,p4 | D. | p2,p3,p4 |
分析 若出現四支球隊并列第一名,則第一名的勝場數不可能為3或者4并列贏兩場,不可能恰有四支球隊并列第一,故p1為真;有可能出現恰有兩支球隊并列第一名,故P25支球隊單循環一共是10場比賽,有210個不同的結果,認為所有不同比賽結果都是等可能的.記有全勝的比賽可能結果為$C_5^1{2^6}$種,有全敗的比賽可能結果為$C_5^1{2^6}$種.既有全勝又有全敗的結果為$A_5^2{2^3}$種,由此求出p3為真;若五支球隊成績并列第一名則必出現a>b>c>d>e>a,同時a>c>e>b>d>a,從而求出五支球隊成績并列第一名的概率為$\frac{48}{{{2^{10}}}}=\frac{3}{64}$.
解答 解:p1為真:因為若出現四支球隊并列第一名,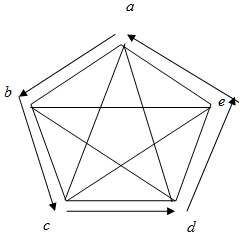
則第一名的勝場數不可能為3或者4(因為如此需要超過10個單場勝利者)并列贏兩場,
那么自然就是五隊同名次,所以不可能恰有四支球隊并列第一.有可能出現恰有兩支球隊并列第一名,p2為真.
p3為真:5支球隊單循環一共是10場比賽,
所以有210個不同的結果,由于勝率都是$\frac{1}{2}$,
故認為所有不同比賽結果都是等可能的.記有全勝的比賽可能結果為$C_5^1{2^6}$種,
有全敗的比賽可能結果為$C_5^1{2^6}$種.既有全勝又有全敗的結果為$A_5^2{2^3}$種,
則既無全勝又無全敗的結果為${2^{10}}-C_5^1{2^6}-C_5^1{2^6}+A_5^2{2^3}$種.
命題p3的概率為$\frac{{2}^{10}-{C}_{5}^{1}•{2}^{6}-{C}_{5}^{1}•{2}^{6}+{A}_{5}^{2}•{2}^{3}}{{2}^{10}}$
=$1-\frac{{5×{2^7}}}{{{2^{10}}}}+\frac{{20×{2^3}}}{{{2^{10}}}}=1-\frac{5}{8}+\frac{5}{32}=\frac{17}{32}$,故p3是正確的.
p4為假:若五支球隊成績并列第一名則必出現a>b>c>d>e>a,
同時a>c>e>b>d>a,
也就是彼得森圖.規定外圈順時針為勝,
那么外圈一共有$\frac{A_5^5}{5}$種不同排列,內圈只有兩種,
故一共有48種,所以概率為$\frac{48}{{{2^{10}}}}=\frac{3}{64}$.
故選:A.
點評 本題考查概率的求法,是中檔題,解題時要認真審題,注意互斥事件概率加法公式、相互獨立事件概率乘法公式的合理運用.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
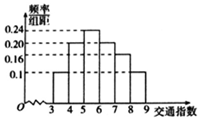 隨著社會發展,廣州市在一天的上下班時段經常會出現堵車嚴重的現象.交通指數是交通擁堵指數的簡稱,是綜合反映道路網暢通或擁堵的概念.記交通指數為T,其范圍為[0,10],分別有5個級別;T∈[0,2)暢通;T∈[2,4)基本暢通;T∈[4,6)輕度擁堵;T∈[6,8)中度擁堵;T∈[8,10)嚴重擁堵.早高峰時段(T≥3),從廣州市交通指揮中心隨機選取了50個交通路段進行調查,依據交通指數數據繪制的直方圖如圖所示:
隨著社會發展,廣州市在一天的上下班時段經常會出現堵車嚴重的現象.交通指數是交通擁堵指數的簡稱,是綜合反映道路網暢通或擁堵的概念.記交通指數為T,其范圍為[0,10],分別有5個級別;T∈[0,2)暢通;T∈[2,4)基本暢通;T∈[4,6)輕度擁堵;T∈[6,8)中度擁堵;T∈[8,10)嚴重擁堵.早高峰時段(T≥3),從廣州市交通指揮中心隨機選取了50個交通路段進行調查,依據交通指數數據繪制的直方圖如圖所示:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
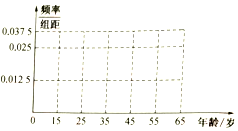 隨著生活水平的提高,人們對空氣質量的要求越來越高,某機構為了解公眾對“車輛限行”的態度,隨機抽查40人,并將調查情況進行整理后制成如表:
隨著生活水平的提高,人們對空氣質量的要求越來越高,某機構為了解公眾對“車輛限行”的態度,隨機抽查40人,并將調查情況進行整理后制成如表:| 年齡(歲) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 頻數 | 5 | 10 | 10 | 5 | 10 |
| 贊成人數 | 4 | 6 | 8 | 4 | 9 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
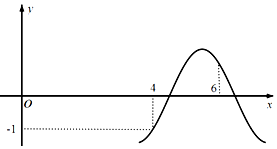
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com