
分析 求出函數(shù)的導(dǎo)數(shù),得到a≠0,△>0,令f′(x),求出方程f′(x)=0的根,通過通過a的范圍,得到關(guān)于a的不等式組,解出即可.
解答 解:由題意可得:f′(x)=3ax2-2x+4,
若函數(shù)f(x)=ax3-x2+4x+3恰有三個零點,
則f′(x)=0有2個不相等的實數(shù)根,
故△=4-48a>0,
令f′(x)=0,解得:x=$\frac{1±\sqrt{1-12a}}{3a}$,
a>0時,x1=$\frac{1-\sqrt{1-12a}}{3a}$<x2=$\frac{1+\sqrt{1-12a}}{3a}$,
只需$\left\{\begin{array}{l}{f{(x}_{1})>0}\\{f{(x}_{2})<0}\end{array}\right.$,解得:0<a<$\frac{14}{243}$,
a<0時,x1=$\frac{1+\sqrt{1-12a}}{3a}$<x2=$\frac{1-\sqrt{1-12a}}{3a}$,
只需$\left\{\begin{array}{l}{f{(x}_{1})>0}\\{f{(x}_{2})<0}\end{array}\right.$,解得:-2<a<0,
故答案為:(-2,0)∪(0,$\frac{14}{243}$).
點評 本題考查了函數(shù)的單調(diào)性、極值問題,考查導(dǎo)數(shù)的應(yīng)用,是一道中檔題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:選擇題
 在幾何體EFABCD中,矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,且AB∥EF,AB=2EF,設(shè)平面CBF將幾何體EFABCD分成的兩個錐體的體積分別為VF-ABCD,VF-CBE,求VF-ABCD:VF-CBE的值為( )
在幾何體EFABCD中,矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,且AB∥EF,AB=2EF,設(shè)平面CBF將幾何體EFABCD分成的兩個錐體的體積分別為VF-ABCD,VF-CBE,求VF-ABCD:VF-CBE的值為( )| A. | 2:1 | B. | 3:1 | C. | 4:1 | D. | 5:1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 24 | B. | 32 | C. | 36 | D. | 40 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | -1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | f($\frac{5}{2}$)<f(1)<f($\frac{7}{2}$) | B. | f(1)<f($\frac{7}{2}$)<f($\frac{5}{2}$) | C. | f($\frac{7}{2}$)<f(1)<f($\frac{5}{2}$) | D. | f($\frac{7}{2}$)<f($\frac{5}{2}$)<f(1) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
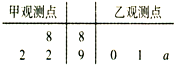 如圖,莖葉圖記錄了某城市甲、乙兩個觀測點連續(xù)三天觀測到的空氣質(zhì)量指數(shù)(AQI).乙觀測點記錄中有一個數(shù)字模糊無法確認(rèn),已知該數(shù)是0,1,…,9中隨機(jī)的一個數(shù),并在圖中以a表示.
如圖,莖葉圖記錄了某城市甲、乙兩個觀測點連續(xù)三天觀測到的空氣質(zhì)量指數(shù)(AQI).乙觀測點記錄中有一個數(shù)字模糊無法確認(rèn),已知該數(shù)是0,1,…,9中隨機(jī)的一個數(shù),并在圖中以a表示.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
| x | 1 | 2 | 3 | 4 |
| y | 0.4 | 0.9 | 1.1 | 1.6 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com