
分析 把直線的方程與橢圓的方程聯立,轉化為關于x的一元二次方程,得到根與系數的關系,假設以CD為直徑的圓過E點,則CE⊥DE,將它們聯立消去x1,x2即可得出k的值.
解答 解:假若存在這樣的k值,由$\left\{\begin{array}{l}y=kx+2\\{x^2}+3{y^2}-3=0\end{array}\right.$得(1+3k2)x2+12kx+9=0.
∴△=(12k)2-36(1+3k2)>0. ①
設C(x1,y1)、D(x2,y2),則$\left\{\begin{array}{l}{x_1}+{x_2}=-\frac{12k}{{1+3{k^2}}}\\{x_1}•{x_2}=\frac{9}{{1+3{k^2}}}\end{array}\right.$②
而${y_1}•{y_2}=(k{x_1}+2)(k{x_2}+2)={k^2}{x_1}{x_2}+2k({x_1}+{x_2})+4$.
要使以CD為直徑的圓過點E(-1,0),當且僅當CE⊥DE時,則$\frac{y_1}{{{x_1}+1}}•\frac{y_2}{{{x_2}+1}}=-1$,即y1y2+(x1+1)(x2+1)=0.
∴(k2+1)x1x2+2(k+1)(x1+x2)+5=0. ③
將②式代入③整理解得$k=\frac{7}{6}$.經驗證,$k=\frac{7}{6}$,使①成立.
綜上可知,存在$k=\frac{7}{6}$,使得以CD為直徑的圓過點E.
點評 本題考查橢圓的標準方程,考查橢圓的性質,考查直線與橢圓的位置關系,考查韋達定理的運用,考查向量知識,解題的關鍵是聯立方程,利用韋達定理求解.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:高中數學 來源: 題型:選擇題
| A. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{4}$) | B. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{4}$] | C. | [0,-$\frac{\sqrt{3}}{4}$] | D. | (-$\frac{2}{3}$,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(a2-a+1)<$f(\frac{3}{4})$ | B. | f(a2-a+1)>$f(\frac{3}{4})$ | C. | f(a2-a+1)≤$f(\frac{3}{4})$ | D. | f(a2-a+1)≥$f(\frac{3}{4})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 顧客人數/商品 | 甲 | 乙 | 丙 | 丁 |
| 100 | √ | × | √ | √ |
| 217 | × | √ | × | √ |
| 200 | √ | √ | √ | × |
| 300 | √ | × | √ | × |
| 85 | √ | × | × | × |
| 98 | × | √ | × | × |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
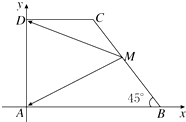 在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=45°,AB=2CD=4,M為腰BC的中點,則$\overrightarrow{MA}$•$\overrightarrow{MD}$=( )
在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=45°,AB=2CD=4,M為腰BC的中點,則$\overrightarrow{MA}$•$\overrightarrow{MD}$=( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,1) | B. | (-∞,1] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
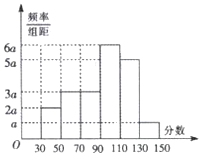 從某市高三數學考試成績中,隨機抽取了60名學生的成績得到頻率分布直方圖如圖:
從某市高三數學考試成績中,隨機抽取了60名學生的成績得到頻率分布直方圖如圖:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com