Question

18．已知梯形ABCD中，AB⊥AD，$\overrightarrow{AB}=3\overrightarrow{DC}，cos∠DAC=\frac{{\sqrt{3}}}{2}，\overrightarrow{BE}=m\overrightarrow{BC}$（0＜m＜1），若|$\overrightarrow{AE}$|²=$|{\overrightarrow{AC}}||{\overrightarrow{AB}}$|，則$\frac{CE}{CB}$=（　　）

• A． $\frac{1+\sqrt{15}}{7}$
• B． $\frac{1}{7}$
• C． $\frac{2}{3}$
• D． $\frac{2+\sqrt{15}}{7}$

Answer 1

分析 建立坐標系，設$\frac{CE}{CB}=λ（0＜λ＜1）$，求出各向量的坐標，列方程解出λ．

解答 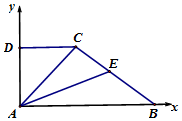解：以A為原點，建立如圖直角坐標系，依題意，∠DAC=30°，
不妨設DC=1，則$AD=\sqrt{3}$，AC=2，AB=3，
故$C（1，\sqrt{3}），B（3，0）$，故$\overrightarrow{CB}=（2，-\sqrt{3}）$，則$|{\overrightarrow{CB}}|=\sqrt{7}$；
設$\frac{CE}{CB}=λ（0＜λ＜1）$，故$\overrightarrow{CE}=（2λ，-\sqrt{3}λ）$，故$E（2λ+1，\sqrt{3}-\sqrt{3}λ）$；
∵${|{\overrightarrow{AE}}|^2}=|{\overrightarrow{AC}}|•|{\overrightarrow{AB}}|$，∴${（2λ+1）^2}+{（{\sqrt{3}-\sqrt{3}λ}）^2}=2×3$，
即7λ²-2λ-2=0，解得$λ=\frac{{1+\sqrt{15}}}{7}$，
故選A．

點評 本題考查了平面向量的數量積運算，屬于中檔題．