
分析 (1)求出函數的導數,通過討論a的范圍,求出函數的單調區間即可;
(2)分離參數a,令$g(x)=-\frac{1}{{{x^2}lnx}}\;,\;x∈(0,1)$,求出函數的導數,從而求出g(x)的最小值,得到a的范圍即可.
解答 解:(1)f(x)的定義域為$(0,+∞),f'(x)=\frac{{a{x^2}-2}}{x^3}$,
①當a≤0時,f'(x)<0,∴f(x)在(0,+∞)上單調遞減;
②$當a>0時,f(x)在(0,\sqrt{\frac{2}{a}})上單調遞減,在(\sqrt{\frac{2}{a}},+∞)上單調遞增$.
(2)$f(x)>0在(0,\;1)上恒成立?a<-\frac{1}{{{x^2}lnx}}在(0,1)恒成立?a<{(-\frac{1}{{{x^2}lnx}})_{min}}$,
令$g(x)=-\frac{1}{{{x^2}lnx}}\;,\;x∈(0,1)$,
則$g'(x)=\frac{2lnx+1}{{{x^3}{{ln}^2}x}}$,
當$x∈(0,{e^{-\frac{1}{2}}})時g'(x)<0,當x∈({e^{-\frac{1}{2}}},1)時g'(x)>0$,
所以,$g(x)在(0,{e^{-\frac{1}{2}}})遞增,在({e^{-\frac{1}{2}}},1)遞減$,
所以,$g{(x)_{min}}=g({e^{-\frac{1}{2}}})=2e$.
因此,a<2e.即實數a的取值范圍是(-∞,2e).
點評 本題考查了函數的單調性、最值問題,考查導數的應用以及分類討論思想,是一道中檔題.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
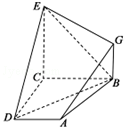 如圖,已知四邊形ABCD和BCEG均為直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2BG=2.
如圖,已知四邊形ABCD和BCEG均為直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2BG=2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com