
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
分析 (1)把所給的四對數據寫成對應的點的坐標,在坐標系中描出來得到散點圖;
(2)計算對應的數值,求出回歸方程的系數,寫出線性回歸方程;
(3)利用線性回歸方程計算x=100時$\stackrel{∧}{y}$的值,再求比技改前降低的噸數.
解答 解:(1)把所給的四對數據寫成對應的點的坐標,在坐標系中描出來,得到散點圖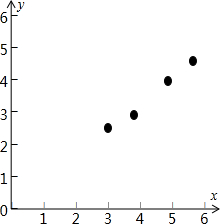 ;
;
(2)計算$\overline{x}$=$\frac{1}{4}$×(3+4+5+6)=4.5,
$\overline{y}$=$\frac{1}{4}$×(2.5+3+4+4.5)=3.5,
$\sum_{i=1}^{4}$${{x}_{i}}^{2}$=32+42+52+62=86,
$\sum_{i=1}^{4}$xiyi=3×2.5+4×3+5×4+6×4.5=66.5,
∴回歸方程的系數為:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$=$\frac{66.5-4×4.5×3.5}{86-4{×4.5}^{2}}$=0.7,
$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=3.5-0.7×4.5=0.35,
∴所求線性回歸方程為$\stackrel{∧}{y}$=0.7x+0.35;
(3)利用線性回歸方程計算x=100時,$\stackrel{∧}{y}$=0.7×100+0.35=70.35,
則90-70.35=19.65,
即比技改前降低了19.65噸.
點評 本題考查了線性回歸方程的求法與應用問題,也考查了散點圖的畫法問題,是基礎題目.


 優生樂園系列答案
優生樂園系列答案 新編小學單元自測題系列答案
新編小學單元自測題系列答案科目:高中數學 來源: 題型:解答題
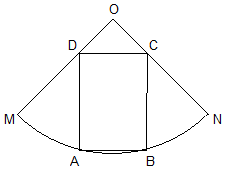 如圖,有一塊扇形草地OMN,已知半徑為R,∠MON=$\frac{π}{2}$,現要在其中圈出一塊矩形場地ABCD作為兒童樂園使用,其中點A、B在弧MN上,且線段AB平行于線段MN
如圖,有一塊扇形草地OMN,已知半徑為R,∠MON=$\frac{π}{2}$,現要在其中圈出一塊矩形場地ABCD作為兒童樂園使用,其中點A、B在弧MN上,且線段AB平行于線段MN查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 患呼吸系統疾病 | 未患呼吸系統疾病 | 總計 | |
| 重污染地區 | 103 | 1 397 | 1 500 |
| 輕污染地區 | 13 | 1 487 | 1 500 |
| 總計 | 116 | 2 884 | 3 000 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 充分必要條件 | ||
| C. | 必要不充分條件 | D. | 既不充分又不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
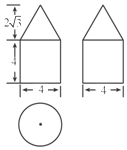 如圖是由圓柱與圓錐組合而成的幾何體的三視圖,則該幾何體的體積為( )
如圖是由圓柱與圓錐組合而成的幾何體的三視圖,則該幾何體的體積為( )| A. | 16π+$\sqrt{3}π$ | B. | 16π+8$\sqrt{3}$π | C. | 16π+$\frac{8}{3}\sqrt{3}π$ | D. | 16π+$\frac{4}{3}\sqrt{3}π$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com