
【題目】已知![]() 為拋物線
為拋物線![]() 的焦點,過
的焦點,過![]() 的動直線交拋物線
的動直線交拋物線![]() 于
于![]() ,
,![]() 兩點.當直線與
兩點.當直線與![]() 軸垂直時,
軸垂直時,![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)設直線![]() 的斜率為1且與拋物線的準線
的斜率為1且與拋物線的準線![]() 相交于點
相交于點![]() ,拋物線
,拋物線![]() 上存在點
上存在點![]() 使得直線
使得直線![]() ,
,![]() ,
,![]() 的斜率成等差數列,求點
的斜率成等差數列,求點![]() 的坐標.
的坐標.
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,上頂點為A,過
,上頂點為A,過![]() 的直線
的直線![]() 與y軸交于點M,滿足
與y軸交于點M,滿足![]() (O為坐標原點),且直線l與直線
(O為坐標原點),且直線l與直線![]() 之間的距離為
之間的距離為![]() .
.
(1)求橢圓C的方程;
(2)在直線![]() 上是否存在點P,滿足
上是否存在點P,滿足![]() ?存在,指出有幾個這樣的點(不必求出點的坐標);若不存在,請說明理由.
?存在,指出有幾個這樣的點(不必求出點的坐標);若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過橢圓![]() 的四個頂點與坐標軸垂直的四條直線圍成的矩形
的四個頂點與坐標軸垂直的四條直線圍成的矩形![]() (
(![]() 是第一象限內的點)的面積為
是第一象限內的點)的面積為![]() ,且過橢圓
,且過橢圓![]() 的右焦點
的右焦點![]() 的傾斜角為
的傾斜角為![]() 的直線過點
的直線過點![]() .
.
(1)求橢圓![]() 的標準方程
的標準方程
(2)若射線![]() 與橢圓
與橢圓![]() 的交點分別為
的交點分別為![]() .當它們的斜率之積為
.當它們的斜率之積為![]() 時,試問
時,試問![]() 的面積是否為定值?若為定值,求出此定值;若不為定值,說明理由.
的面積是否為定值?若為定值,求出此定值;若不為定值,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于數列![]() 、
、![]() ,把和
,把和![]() 叫做數列
叫做數列![]() 與
與![]() 的前
的前![]() 項泛和,記作為
項泛和,記作為![]() .已知數列
.已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)數列![]() 與數列
與數列![]() 的前
的前![]() 項的泛和為
項的泛和為![]() ,且
,且![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)從數列![]() 的前
的前![]() 項中,任取
項中,任取![]() 項從小到大依次排列,得到數列
項從小到大依次排列,得到數列![]() 、
、![]() 、
、![]() 、
、![]() ;再將余下的
;再將余下的![]() 項從大到小依次排列,得到數列
項從大到小依次排列,得到數列![]() 、
、![]() 、
、![]() 、
、![]() .求數列
.求數列![]() 與數列
與數列![]() 的前
的前![]() 項的泛和
項的泛和![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
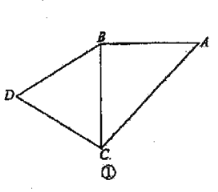
【題目】如圖①,![]() 是以
是以![]() 為斜邊的等腰直角三角形,
為斜邊的等腰直角三角形,![]() 是等邊三角形,
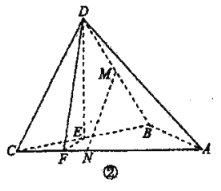
是等邊三角形,![]() ,如圖②,將
,如圖②,將![]() 沿
沿![]() 折起使平面
折起使平面![]() 平面
平面![]() 分別為
分別為![]() 的中點,點
的中點,點![]() 在棱
在棱![]() 上,且
上,且![]() ,點
,點![]() 在棱
在棱![]() 上,且
上,且![]() .
.
(1)在棱![]() 上是否存在一點
上是否存在一點![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(2)求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車的投放,方便了市民短途出行,被譽為中國“新四大發明”之一.某市為研究單車用戶與年齡的相關程度,隨機調查了100位成人市民,統計數據如下:
不小于40歲 | 小于40歲 | 合計 | |
單車用戶 | 12 | 18 | 30 |
非單車用戶 | 38 | 32 | 70 |
合計 | 50 | 50 | 100 |
(1)從獨立性檢驗角度分析,能否有![]() 以上的把握認為該市成人市民是否為單車用戶與年齡是否小于40歲有關;
以上的把握認為該市成人市民是否為單車用戶與年齡是否小于40歲有關;
(2)將此樣本的頻率做為概率,從該市單車用戶中隨機抽取3人,記不小于40歲的單車用戶的人數為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
下面臨界值表供參考:
P( | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式: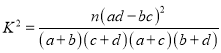 ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com