
已知命題p:方程x2+mx+1=0有兩個不相等的實根;q:不等式4x2+4(m–2)x+1>0的解集為R;若p或q為真,p且q為假,求實數m的取值范圍。
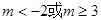 或
或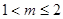
解析試題分析:研究四種命題關系,首先研究各命題為真時的充要條件,因為方程x2+mx+1=0有兩個不相等的實根,,所以Δ1=m2–4>0,m>2或m<–2;又因為不等式4x2+4(m–2)x+1>0的解集為R,所以Δ2=16(m–2)2–16<0, ∴1<m<3,其次研究復合命題真假性,確定簡單命題真假性,因為p或q為真,p且q為假,所以p與q為一真一假,對于命題為假的情形,取命題為真時范圍的補集,本題分兩組求解,取其并集.
試題解析:解:因為方程x2+mx+1=0有兩個不相等的實根,
所以Δ1=m2–4>0,∴m>2或m<–2
又因為不等式4x2+4(m–2)x+1>0的解集為R,
所以Δ2=16(m–2)2–16<0,∴1<m<3 .5分
因為p或q為真,p且q為假,所以p與q為一真一假,
(1)當p為真q為假時,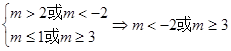
(2)當p為假q為真時,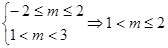
綜上所述得:m的取值范圍是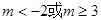 或
或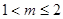 .10分
.10分
考點:四種命題關系,二次函數、二次方程、二次不等式之間關系


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案 新思維寒假作業系列答案
新思維寒假作業系列答案科目:高中數學 來源: 題型:解答題
已知p:方程x2+mx+1=0有兩個不等的負實根,q:方程4x2+4(m﹣2)x+1=0無實根.若“p或q”為真,“p且q”為假.求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知 ,設p:函數
,設p:函數 在(0,+∞)上單調遞減,
在(0,+∞)上單調遞減,
q:曲線y=x2+(2a 3)x+1與x軸交于不同的兩點.若“p且q”為假,“﹁q”為假,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
下列說法:(1)命題“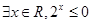 ”的否定是“
”的否定是“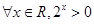 ”;
”;
(2)關于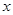 的不等式
的不等式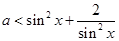 恒成立,則
恒成立,則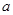 的取值范圍是
的取值范圍是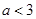 ;
;
(3)對于函數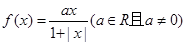 ,則有當
,則有當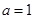 時,
時,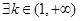 ,使得函數
,使得函數 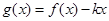 在
在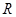 上有三個零點;
上有三個零點;
(4)
(5)已知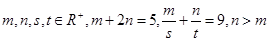 ,且
,且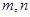 是常數,又
是常數,又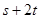 的最小值是
的最小值是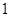 ,則
,則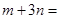 7.其中正確的個數是 .
7.其中正確的個數是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com