
分析 (I)曲線C1:ρ=2cosθ,即ρ2=2ρcosθ,利用互化公式可得直角坐標方程.曲線${C_2}:ρ{sin^2}θ=4cosθ$,即ρ2sin2θ=4ρcosθ,利用互化公式可得直角標準方程.
(II)設四點在C上的排列順次為P,Q,R,S,其參數分別為t1,t2,t3,t4.曲線C的參數方程代入拋物線方程可得:3t2-8t-32=0.△1>0,可得t1+t4.曲線C的參數方程代入圓的方程可得:t2+t=0.△2>0,可得t2+t3.∴||PQ|-|RS||=|(t2-t1)-(t4-t3)|=|(t2+t3)-(t1+t4)|即可得出.
解答 解:(Ⅰ)∵曲線C1:ρ=2cosθ,即ρ2=2ρcosθ,
∴曲線C1的直角坐標方程為:x2+y2-2x=0,
∵曲線${C_2}:ρ{sin^2}θ=4cosθ$,即ρ2sin2θ=4ρcosθ,
∴曲線C2的直角坐標方程為:y2=4x.
(Ⅱ)設四點在C上的排列順序為P,Q,R,S,其參數分別為t1,t2,t3,t4.
曲線C的參數方程$\left\{{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$(t為參數)代入拋物線方程y2=4x,
可得:3t2-8t-32=0.△1>0,可得t1+t4=$\frac{8}{3}$.
曲線C的參數方程$\left\{{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$(t為參數)代入圓的方程可得:t2+t=0.△2>0,可得t2+t3=-1.
∴||PQ|-|RS||=|(t2-t1)-(t4-t3)|=|(t2+t3)-(t1+t4)|=|1+$\frac{8}{3}$|=$\frac{11}{3}$.
故答案為:$\frac{11}{3}$.
點評 本題考查曲線與坐標軸的交點坐標的求法,考查極坐標方程、直角坐標方程、參數方程的互化等基礎知識,考查推理論證能力、運算求解能力,考查化歸與轉化思想、函數與方程思想,是中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
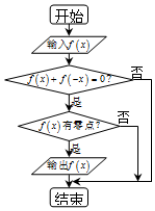 某流程圖如圖所示,現輸入如下四個函數,則可以輸出的函數是①②③.
某流程圖如圖所示,現輸入如下四個函數,則可以輸出的函數是①②③.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 優秀 | 非優秀 | 總計 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 總計 | 105 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com