
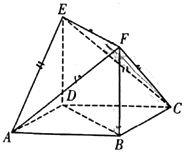
【題目】如圖所示的多面體中,![]() 是菱形,
是菱形,![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求證:平面![]() 平面
平面 ![]() ;
;
(2)在線段![]() 上取一點
上取一點![]() ,當二面角
,當二面角![]() 的大小為
的大小為![]() 時,求
時,求![]() .
.
【答案】(1)見證明;(2) ![]()
【解析】
(1)取AE的中點M,先證明∠AMC就是二面角A-EF-C的平面角,再證明![]() ,即證平面
,即證平面![]() 平面
平面 ![]() ;(2)以AC與BD交點O為坐標原點,0A、OB分別為
;(2)以AC與BD交點O為坐標原點,0A、OB分別為![]() 軸建立直角坐標系,設
軸建立直角坐標系,設![]() ,利用向量法求得
,利用向量法求得![]() ,解方程即得
,解方程即得![]() .
.
解:(1)取AE的中點M.由于ED⊥面ABCD,ED//FB,
∴DE⊥AD,ED⊥DC,FB⊥BC,FB⊥AB,又ABCD是菱形,BDEF是矩形,
所以△ADE,△CDE,△ABF,△CBF是全等直角三角形,AE=AF,CE=CF,
所以AM⊥EF,CM⊥EF,∠AMC就是二面角A-EF-C的平面角
經計算![]() ,
,![]() ,
,
所以![]() ,即
,即![]() .
.
所以平面AEF⊥平面CEF.
(2)以AC與BD交點O為坐標原點,0A、OB分別為![]() 軸建立直角坐標系,由AD=BD=2,則A(
軸建立直角坐標系,由AD=BD=2,則A(![]() ,0,0),M(0,O,
,0,0),M(0,O,![]() ),C(﹣
),C(﹣![]() ,0,0),E(0,﹣1,
,0,0),E(0,﹣1,![]() ),
),
F(0,1,![]() ),
),![]() .
.
平面CEF的一個法向量![]() .
.
設![]() ,則
,則![]() ,
,
![]() ,
,![]()
設平面NEF的法向量![]() ,則
,則
得![]() ,
,
令![]() ,則
,則![]() ,得
,得![]() .
.
因為二面角![]() 的大小為60°,
的大小為60°,
所以![]() ,
,
![]() 整理得
整理得![]() ,解得
,解得![]()
所以![]() .
.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:
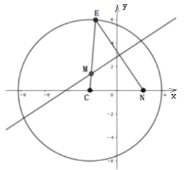
【題目】已知點![]() ,在圓
,在圓![]() :
:![]() 上任取一點
上任取一點![]() ,
,![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() .(如圖).
.(如圖).
(1)求點![]() 的軌跡方程
的軌跡方程![]() ;
;
(2)若過點![]() 的動直線
的動直線![]() 與(1)中的軌跡
與(1)中的軌跡![]() 相交于
相交于![]() 、
、![]() 兩點.問:平面內是否存在異于點
兩點.問:平面內是否存在異于點![]() 的定點
的定點![]() ,使得
,使得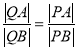 恒成立?試證明你的結論.
恒成立?試證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的傾斜角為
的傾斜角為![]() ,且經過點
,且經過點![]() .以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,直線
.以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,直線![]() ,從原點O作射線交
,從原點O作射線交![]() 于點M,點N為射線OM上的點,滿足
于點M,點N為射線OM上的點,滿足![]() ,記點N的軌跡為曲線C.
,記點N的軌跡為曲線C.
(Ⅰ)求出直線![]() 的參數方程和曲線C的直角坐標方程;
的參數方程和曲線C的直角坐標方程;
(Ⅱ)設直線![]() 與曲線C交于P,Q兩點,求
與曲線C交于P,Q兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C經過點A(2,-1),和直線x+y=1相切,且圓心在直線y=-2x上.
(1)求圓C的方程;
(2)已知直線l經過(2,0)點,并且被圓C截得的弦長為2,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列推理不屬于合情推理的是( )
A. 由銅、鐵、鋁、金、銀等金屬能導電,得出一切金屬都能導電.
B. 半徑為![]() 的圓面積
的圓面積![]() ,則單位圓面積為
,則單位圓面積為![]() .
.
C. 由平面三角形的性質推測空間三棱錐的性質.
D. 猜想數列2,4,8,…的通項公式為![]() .
. ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體![]() 中,點
中,點![]() 是棱
是棱![]() 上的一個動點,平面
上的一個動點,平面![]() 交棱
交棱![]() 于點
于點![]() .下列命題正確的為_______________.
.下列命題正確的為_______________.

①存在點![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②對于任意的點![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在點![]() ,使得
,使得![]() 平面
平面![]() ;
;
④對于任意的點![]() ,四棱錐
,四棱錐![]() 的體積均不變.
的體積均不變.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】西安市自2017年5月啟動對“車不讓人行為”處罰以來,斑馬線前機動車搶行不文明行為得以根本改變,斑馬線前禮讓行人也成為了一張新的西安“名片”.
但作為交通重要參與者的行人,闖紅燈通行卻頻有發生,帶來了較大的交通安全隱患及機動車通暢率降低,交警部門在某十字路口根據以往的檢測數據,得到行人闖紅燈的概率約為0.4,并從穿越該路口的行人中隨機抽取了200人進行調查,對是否存在闖紅燈情況得到![]() 列聯表如下:
列聯表如下:
30歲以下 | 30歲以上 | 合計 | |
闖紅燈 | 60 | ||
未闖紅燈 | 80 | ||
合計 | 200 |
近期,為了整頓“行人闖紅燈”這一不文明及項違法行為,交警部門在該十字路口試行了對闖紅燈行人進行經濟處罰,并從試行經濟處罰后穿越該路口行人中隨機抽取了200人進行調查,得到下表:
處罰金額 | 5 | 10 | 15 | 20 |
闖紅燈的人數 | 50 | 40 | 20 | 0 |
將統計數據所得頻率代替概率,完成下列問題.
(Ⅰ)將![]() 列聯表填寫完整(不需寫出填寫過程),并根據表中數據分析,在未試行對闖紅燈行人進行經濟處罰前,是否有99.9%的把握認為闖紅燈與年齡有關;
列聯表填寫完整(不需寫出填寫過程),并根據表中數據分析,在未試行對闖紅燈行人進行經濟處罰前,是否有99.9%的把握認為闖紅燈與年齡有關;
(Ⅱ)當處罰金額為10元時,行人闖紅燈的概率會比不進行處罰降低多少;
(Ⅲ)結合調查結果,談談如何治理行人闖紅燈現象.
參考公式:![]() ,其中
,其中![]()
參考數據:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.132 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() 的坐標為
的坐標為![]() ,拋物線
,拋物線![]() 的方程為
的方程為![]() ,過
,過![]() 作動直線
作動直線![]() 交拋物線于
交拋物線于![]() 兩點,設線段
兩點,設線段![]() 的中點為
的中點為![]() .
.
(1)若![]() 與
與![]() 重合,求直線
重合,求直線![]() 的方程;
的方程;
(2)求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com