
分析 (1)由題意可得b=$\sqrt{3}$,運用直角三角形正弦函數可得a=2,進而得到橢圓方程;
(2)設P(x1,y1),M(2,y0),求出A,B坐標,運用三點共線的條件:斜率相等,求得直線m的方程,由恒過定點方法,即可得證.
解答 解:(1)由條件∠OF2B=60°,
可得|BF2|=$\frac{\sqrt{3}}{sin60°}$=2,
則$a=2,b=\sqrt{3}$,
故所求橢圓方程為$\frac{x^2}{4}+\frac{y^2}{3}=1$;
( 2 )證明:設P(x1,y1),M(2,y0),直線l:x=2,
A(-2,0),由A,P,M共線可得$\frac{{y}_{1}}{{x}_{1}+2}$=$\frac{{y}_{0}}{4}$,
直線BP的斜率為k2=$\frac{{y}_{1}}{{x}_{1}-2}$,直線m的斜率為km=$\frac{2-{x}_{1}}{{y}_{1}}$,
則直線m的方程為y-y0=$\frac{2-{x}_{1}}{{y}_{1}}$(x-2),
即y=$\frac{2-{x}_{1}}{{y}_{1}}$(x-2)+y0=$\frac{2-{x}_{1}}{{y}_{1}}$(x-2)+$\frac{4{y}_{1}}{{x}_{1}+2}$
=$\frac{2-{x}_{1}}{{y}_{1}}$[(x-2)+$\frac{4{{y}_{1}}^{2}}{4-{{x}_{1}}^{2}}$]
=$\frac{2-{x}_{1}}{{y}_{1}}$[(x-2)+$\frac{12-3{{x}_{1}}^{2}}{4-{{x}_{1}}^{2}}$]=$\frac{2-{x}_{1}}{{y}_{1}}$(x+1),
當x=-1時,y=0.
所以直線m過定點(-1,0).
點評 本題考查橢圓方程的求法,以及直線恒過定點的求法,注意運用直線方程和三點共線的條件:斜率相等,考查化簡整理的運算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
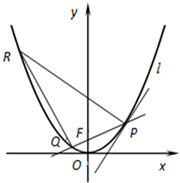 如圖,點F是拋物線C:x2=2y的焦點,點P(x1,y1)為拋物線上的動點(P在第一象限),直線PF交拋物線C于另一點Q,直線l與拋物線C相切于點P.過點P作直線l的垂線交拋物線C于點R.
如圖,點F是拋物線C:x2=2y的焦點,點P(x1,y1)為拋物線上的動點(P在第一象限),直線PF交拋物線C于另一點Q,直線l與拋物線C相切于點P.過點P作直線l的垂線交拋物線C于點R.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com