
分析 (1)利用a1,a2,a3-$\frac{1}{8}$成等差數列.建立等量關系式,求出通項公式.;
(2)寫出數列{bn}的通項公式,然后寫出前n項和的表達式通過錯位相減法求解即可.
解答 解:(1)設等比數列{an}公比為q,
∵${a_1}=\frac{1}{2}$,${a_1},{a_2},{a_3}-\frac{1}{8}$成等差數列,
∴$2{a_2}={a_1}+{a_3}-\frac{1}{8}$,即$2{a_1}q={a_1}+{a_1}{q^2}-\frac{1}{8}$,
整理得4q2-8q+3=0,
解得$q=\frac{1}{2}$或$q=\frac{3}{2}$.
又∵q∈(0,1),
∴$q=\frac{1}{2}$,
∴${a_n}=\frac{1}{2}•{({\frac{1}{2}})^{n-1}}=\frac{1}{2^n}$.
(2)根據題意得bn=2nan=$\frac{2n}{2^n}=\frac{n}{{{2^{n-1}}}}$,${S_n}=1+1+\frac{3}{2^2}+…+\frac{n-1}{{{2^{n-2}}}}+\frac{n}{{{2^{n-1}}}}$,①
$2{S_n}=2+2+\frac{3}{2}+…+\frac{n-1}{{{2^{n-3}}}}+\frac{n}{{{2^{n-2}}}}$,②
②-①得:${S_n}=2+1+\frac{1}{2}+\frac{1}{2^2}…+\frac{1}{{{2^{n-2}}}}-\frac{n}{{{2^{n-1}}}}$
=$2+(1+\frac{1}{2}+\frac{1}{2^2}…+\frac{1}{{{2^{n-2}}}})-\frac{n}{{{2^{n-1}}}}$
=$2+\frac{{1-\frac{1}{{{2^{n-1}}}}}}{{1-\frac{1}{2}}}-\frac{n}{{{2^{n-1}}}}$
=$4-\frac{n+2}{{{2^{n-1}}}}$.
點評 本題考查的知識要點:數列的通項公式的求法,數列的前n項和的應用,屬于基礎題型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3π}{2}$ | B. | 2π | C. | 6π | D. | $\sqrt{6}$π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,2) | B. | (-2,0) | C. | (0,4) | D. | (-1,0) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
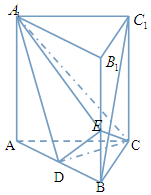 如圖,在直三棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如圖,在直三棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com