
分析 (1)首先直接對f(x)求導,利用f'(1)=2,f'(6)=2列出方程組可求出a與b值;
(2)直接利用導函數求出零點判斷原函數的單調性即可,從而可求出最值;
解答 解:(I)因f(x)=ax2-bx+6lnx+15,
所以f'(x)=2ax-b+$\frac{6}{x}$,
由題意得,f'(1)=2,f'(6)=2得$\left\{\begin{array}{l}{2a-b+6=2}\\{12a-b+1=2}\end{array}\right.$,
故a=$\frac{1}{2}$,b=5.
(II)由(1)知,f(x)=$\frac{1}{2}{x}^{2}$-5x+6lnx+15(x>0),
f′(x)=x-5+$\frac{6}{x}$=$\frac{(x-2)(x-3)}{x}$.
令f′(x)=0,解得x1=2,x2=3.
當0<x<2或x>3時,f′(x)>0,故f(x)在(0,2),(3,+∞)上為增函數;
當2<x<3時,f′(x)<0,故f(x)在(2,3)上為減函數.
由此可知f(x)在x=2處取得極大值f(2)=7+6ln 2,
在x=3處取得極小值f(3)=$\frac{9}{2}$+6ln 3.
點評 本題主要考查了利用導函數判斷函數的單調性與求最值,以及導數定義的理解,屬中等題.


科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
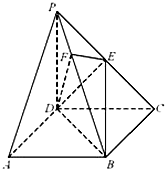 《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.
《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
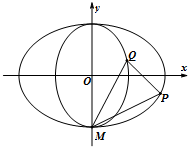 如圖,中心在坐標原點,焦點分別在x軸和y軸上的橢圓T1,T2都過點M(0,-$\sqrt{2}$),且橢圓T1與T2的離心率均為$\frac{\sqrt{2}}{2}$.
如圖,中心在坐標原點,焦點分別在x軸和y軸上的橢圓T1,T2都過點M(0,-$\sqrt{2}$),且橢圓T1與T2的離心率均為$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3π}{2}$ | B. | 2π | C. | 6π | D. | $\sqrt{6}$π |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com