
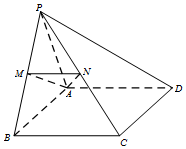
 在四棱錐P-ABCD中,△PAB為正三角形,四邊形ABCD為矩形,平面PAB⊥平面ABCD,AB=2AD,M、N分別為PB、PC的中點.
在四棱錐P-ABCD中,△PAB為正三角形,四邊形ABCD為矩形,平面PAB⊥平面ABCD,AB=2AD,M、N分別為PB、PC的中點.分析 (Ⅰ)MN是△ABC的中位線,可得MN∥BC∥AD,即可證以MN∥平面PAD.
(Ⅱ)過點P作PO垂直于AB,交AB于點O,因為平面PAB⊥平面ABCD,所以PO⊥平面ABCD,如圖建立空間直角坐標系設AB=2,則A(-1,0,0),C(1,1,0),M($\frac{1}{2}$,0,$\frac{\sqrt{3}}{2}$),B(1,0,0),N($\frac{1}{2}$,$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),利用向量法求解.
解答 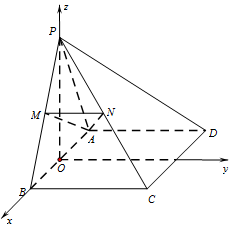 解:(Ⅰ)證明:∵M,N分別是PB,PC中點
解:(Ⅰ)證明:∵M,N分別是PB,PC中點
∴MN是△ABC的中位線∴MN∥BC∥AD
又∵AD?平面PAD,MN?平面PAD
所以MN∥平面PAD.…(5分)
(Ⅱ)過點P作PO垂直于AB,交AB于點O,
因為平面PAB⊥平面ABCD,所以PO⊥平面ABCD,
如圖建立空間直角坐標系設AB=2,則A(-1,0,0),C(1,1,0),M($\frac{1}{2}$,0,$\frac{\sqrt{3}}{2}$),
B(1,0,0),N($\frac{1}{2}$,$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),則$\overrightarrow{AC}=(2,1,0)$,$\overrightarrow{AM}=(\frac{3}{2},0,\frac{\sqrt{3}}{2})$.
設平面CAM法向量為$\overrightarrow{{n}_{1}}=({x}_{1},{y}_{1},{z}_{1})$,由$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{AC}=2{x}_{1}+{y}_{1}=0}\\{\overrightarrow{{n}_{2}}•\overrightarrow{AM}=\frac{3}{2}{x}_{1}+\frac{\sqrt{3}}{2}{z}_{1}=0}\end{array}\right.$ 可得$\overrightarrow{{n}_{1}}=(1,-2,-\sqrt{3}$)
平面ABM法向量$\overrightarrow{{n}_{2}}=(0,1,0)$,∴cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$>=-$\frac{\sqrt{2}}{2}$
因為二面角B-AM-C是銳二面角,
所以二面角B-AM-C等于$\frac{π}{4}$…(12分)
點評 本題考查了空間線面平行的判定,向量法求二面角,屬于中檔題.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | $\frac{27}{2}$ | B. | 27 | C. | $27\sqrt{2}$ | D. | $27\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com