
【題目】數學家歐拉在1765年提出:三角形的外心、重心位于同一直線上,這條直線被后人稱之為三角形的歐拉線,若![]() 的頂點
的頂點![]() ,
,![]() ,且
,且![]() 的歐拉線的方程為
的歐拉線的方程為![]() .
.
(1)求![]() 外心
外心![]() (外接圓圓心)的坐標;
(外接圓圓心)的坐標;
(2)求頂點![]() 的坐標.
的坐標.
(注:如果![]() 三個頂點坐標分別為
三個頂點坐標分別為![]() ,
,![]() ,
,![]() ,則
,則![]() 重心的坐標是
重心的坐標是![]() .)
.)
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)三角形外心是三邊中垂線的交點,由已知條件知頂點![]() ,
,![]() ,計算出
,計算出![]() 邊上的中垂線,結合三角形的歐拉線,聯立方程組求出外心坐標;
邊上的中垂線,結合三角形的歐拉線,聯立方程組求出外心坐標;
(2)由題意知重心也在歐拉線上,設出頂點![]() 的坐標,表示出重心坐標代入歐拉線方程,再結合(1)中的外心坐標,外心到三個頂點距離相等,得到方程組求出頂點
的坐標,表示出重心坐標代入歐拉線方程,再結合(1)中的外心坐標,外心到三個頂點距離相等,得到方程組求出頂點![]() 的坐標.
的坐標.
(1)三角形外心是三邊中垂線的交點,
由已知條件知頂點![]() ,
,![]() ,則
,則![]() 中點坐標為
中點坐標為![]() ,
,![]() ,
,
所以![]() 邊上的中垂線方程為
邊上的中垂線方程為![]() ,化簡得
,化簡得![]() ,
,
又因為三角形的外心在歐拉線上,聯立![]() ,解得
,解得![]() ,
,
所以![]() 外心
外心![]() 的坐標為
的坐標為![]() ;
;
(2)設![]() ,則
,則![]() 的重心坐標為
的重心坐標為![]() ,
,
由題意可知重心在歐拉線上,故滿足![]() ,化簡得
,化簡得![]() ,
,
由(1)得![]() 外心
外心![]() 的坐標為
的坐標為![]() ,
,
則![]() ,即
,即![]() ,
,
整理得![]() ,
,
聯立![]() ,解得
,解得![]() 或
或![]() ,
,
當![]() ,
,![]() 時,點
時,點![]() 與點
與點![]() 重合,故舍去,
重合,故舍去,
所以頂點![]() 的坐標為
的坐標為![]() .
.


科目:高中數學 來源: 題型:
【題目】某商場周年慶,準備提供一筆資金,對消費滿一定金額的顧客以參與活動的方式進行獎勵.顧客從一個裝有大小相同的2個紅球和4個黃球的袋中按指定規則取出2個球,根據取到的紅球數確定獎勵金額,具體金額設置如下表:
取到的紅球數 | 0 | 1 | 2 |
獎勵(單位:元) | 5 | 10 | 50 |
現有兩種取球規則的方案:
方案一:一次性隨機取出2個球;
方案二:依次有放回取出2個球.
(Ⅰ)比較兩種方案下,一次抽獎獲得50元獎金概率的大小;
(Ⅱ)為使得盡可能多的人參與活動,作為公司的負責,你會選擇哪種方案?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如右圖,一個直徑為1的小圓沿著直徑為2的大圓內壁的逆時針方
向滾動,M和N是小圓的一條固定直徑的兩個端點.那么,當小圓這
樣滾過大圓內壁的一周,點M,N在大圓內所繪出的圖形大致是( )
A.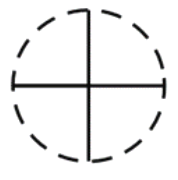 B.
B.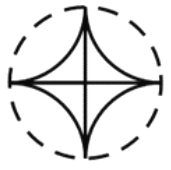
C. D.
D.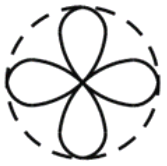
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了考查某廠2000名工人的生產技能情況,隨機抽查了該廠![]() 名工人某天的產量(單位:件),整理后得到如下的頻率分布直方圖(產量的區間分別為:
名工人某天的產量(單位:件),整理后得到如下的頻率分布直方圖(產量的區間分別為:![]() ),其中產量在
),其中產量在![]() 的工人有6名.
的工人有6名.
(1)求這一天產量不小于25的工人數;
(2)該廠規定從產量低于20件的工人中選取2名工人進行培訓,求這兩名工人不在同一分組的概率.
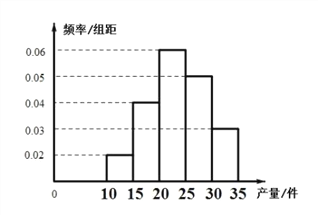
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市有兩家共享單車公司,在市場上分別投放了黃、藍兩種顏色的單車,已知黃、藍兩種顏色的單車的投放比例為2:1.監管部門為了了解兩種顏色的單車的質量,決定從市場中隨機抽取5輛單車進行體驗,若每輛單車被抽取的可能性相同.
(1)求抽取的5輛單車中有2輛是藍色顏色單車的概率;
(2)在騎行體驗過程中,發現藍色單車存在一定質量問題,監管部門決定從市場中隨機地抽取一輛送技術部門作進一步抽樣檢測,并規定若抽到的是藍色單車,則抽樣結束,若抽取的是黃色單車,則將其放回市場中,并繼續從市場中隨機地抽取下一輛單車,并規定抽樣的次數最多不超過![]() (
(![]() )次.在抽樣結束時,已取到的黃色單車以
)次.在抽樣結束時,已取到的黃色單車以![]() 表示,求
表示,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】保護環境,防治環境污染越來越得到人們的重視,某企業在現有設備下每日生產總成本![]() (單位:萬元)與日產量
(單位:萬元)與日產量![]() (單位:噸)之間的函數關系式為
(單位:噸)之間的函數關系式為![]() .現為了減少大氣污染,該企業引進了除塵設備,每噸產品除塵費用為
.現為了減少大氣污染,該企業引進了除塵設備,每噸產品除塵費用為![]() 萬元,除塵后,當日產量
萬元,除塵后,當日產量![]() 時,每日生產總成本
時,每日生產總成本![]() .
.
(1)求![]() 的值;
的值;
(2)若每噸產品出廠價為48萬元,試求除塵后日產量為多少噸時,每噸產品的利潤最大,最大利潤為多少萬元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com