
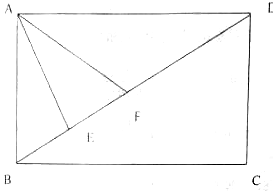
 小王大學畢業后決定利用所學知識自主創業,在一塊矩形的空地上辦起了養殖場,如圖所示,四邊形ABCD為矩形,AB=200米,AD=200$\sqrt{3}$米,現為了養殖需要,在養殖場內要建造蓄水池,小王因地制宜,建造了一個三角形形狀的蓄水池,其中頂點分別為A,E,F(E,F兩點在線段BD上),且∠EAF=$\frac{π}{6}$,設∠BAE=α.
小王大學畢業后決定利用所學知識自主創業,在一塊矩形的空地上辦起了養殖場,如圖所示,四邊形ABCD為矩形,AB=200米,AD=200$\sqrt{3}$米,現為了養殖需要,在養殖場內要建造蓄水池,小王因地制宜,建造了一個三角形形狀的蓄水池,其中頂點分別為A,E,F(E,F兩點在線段BD上),且∠EAF=$\frac{π}{6}$,設∠BAE=α.分析 (1)先求出α的范圍,再分別根據正弦定理得到AE,AF,再根據三角形的面積公式即可表示出f(α),
(2)根據正弦函數的圖象和性質即可求出最值.
解答 解:(1)∵∠BCD=$\frac{π}{2}$,∠EAF=$\frac{π}{6}$,設∠BAE=α∈[0,$\frac{π}{3}$],
在△ABD中,AD=200米,AD=200$\sqrt{3}$米,∠BCD=$\frac{π}{2}$,
∴∠ABD=$\frac{π}{3}$,
在△ABF中,∠AFB=π-∠ABF-∠BAF=π-$\frac{π}{3}$-($\frac{π}{6}$+α)=$\frac{π}{2}$-α,
由正弦定理得:$\frac{AF}{sin∠ABF}$=$\frac{AB}{sin∠AFB}$=$\frac{AB}{sin(\frac{π}{2}-α)}$=$\frac{AB}{cosα}$,
∴AF=$\frac{100\sqrt{3}}{cosα}$,
在△ABE中,由正弦定理得:$\frac{AE}{sin∠ABE}$=$\frac{AB}{sin∠AEB}$=$\frac{AB}{sin(\frac{π}{3}+α)}$,
∴AE=$\frac{100\sqrt{3}}{sin(\frac{π}{3}+α)}$,
則△AEF的面積S△AEF=$\frac{1}{2}$AE•AF•sin∠EAF=$\frac{7500}{sin(\frac{π}{3}+α)cosα}$=$\frac{3000}{2sin(2α+\frac{π}{3})+\sqrt{3}}$,α∈[0,$\frac{π}{3}$],
∴f(α)=$\frac{3000}{2sin(2α+\frac{π}{3})+\sqrt{3}}$,α∈[0,$\frac{π}{3}$],
(2)∵α∈[0,$\frac{π}{3}$],
∴(2α+$\frac{π}{3}$)∈[$\frac{π}{3}$,π].
∴0≤sin(2α+$\frac{π}{3}$)≤1,
∴2sin(2α+$\frac{π}{3}$)+$\sqrt{3}$的最小值為$\sqrt{3}$,
∴當α=$\frac{π}{3}$時,f(α)max=1000$\sqrt{3}$
點評 本題考查了正弦定理和以及三角形的面積公式和正弦函數的圖象和性質,考查了學生分析問題解決問題的能力,屬于中檔題


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 圓錐所有的軸截面是全等的等腰三角形 | |
| B. | 圓柱的軸截面是過母線的截面中面積最大的一個 | |
| C. | 圓錐的軸截面是所有過頂點的界面中面積最大的一個 | |
| D. | 當球心到平面的距離小于球面半徑時,球面與平面的交線總是一個圓 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}或\frac{2π}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com