
分析 (1)求出函數的導數,得到關于a,b的方程組,求出a,b的值即可;(2)求出函數的導數,根據函數的單調性求出f(x)的最小值,求出c的范圍即可.
解答 解:(1)$f'(x)=2a+\frac{b}{x^2}+\frac{4}{x}$$f(x)=2ax-\frac{b}{x}+4lnx$,
在$x=1與x=\frac{1}{3}$處都取得極值,
$\begin{array}{l}f'(1)=0,f'(\frac{1}{3})=0\\∴\left\{\begin{array}{l}2a+b+4=0\\ 2a+9b+12=0\end{array}\right.\end{array}$,
解得:a=-$\frac{3}{2}$,b=-1; 經檢驗符合題意;
(2)由(1)可知,$f(x)=-3x+\frac{1}{x}+4lnx$,
$f'(x)=-3-\frac{1}{x^2}+\frac{4}{x}=-\frac{(3x-1)(x-1)}{x^2}$,
由f'(x)>0,得f(x)的單調增區間為[$\frac{1}{3}$,1],
由f'(x)<0,得f(x)的單調減區間為$(0,\frac{1}{3}]和[1,+∞)$,
∴x=1是f(x)的極大值點 當$x∈[\frac{1}{e},e]$時,$f(\frac{1}{e})$=e-$\frac{3}{e}$-5,f(e)=-3e+$\frac{1}{e}$+4,
而$f(\frac{1}{e})$-f(e)=4e-9-$\frac{4}{e}$>0,所以$f(\frac{1}{e})$>f(e),
即f(x)在$x∈[\frac{1}{e},e]$上的最小值為$\frac{1}{e}$+4-3e,
要使對$x∈[\frac{1}{e},e]$時,f(x)≥c恒成立,
故$c≤f{(x)_{min}}=\frac{1}{e}+4-3e$.
點評 本題考查了函數的單調性、最值問題,考查導數的應用以及分類討論思想,轉化思想,是一道中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 做米飯需要刷鍋,淘米,添水,加熱這些步驟 | |
| B. | 洗衣機的使用說明書 | |
| C. | 利用公式S=πr2計算半徑為4的圓的面積,就是計算π×42 | |
| D. | 解方程2x2+x-1=0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2$\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -6 | B. | $-\frac{3}{8}$ | C. | 6 | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
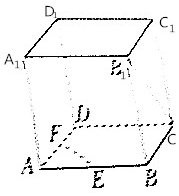 如圖所示,在正方體ABCD-A1B1C1D1中,E、F分別是AB、AD的中點,則異面直線B1C與EF所成的角的大小為( )
如圖所示,在正方體ABCD-A1B1C1D1中,E、F分別是AB、AD的中點,則異面直線B1C與EF所成的角的大小為( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
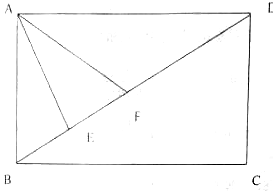 小王大學畢業后決定利用所學知識自主創業,在一塊矩形的空地上辦起了養殖場,如圖所示,四邊形ABCD為矩形,AB=200米,AD=200$\sqrt{3}$米,現為了養殖需要,在養殖場內要建造蓄水池,小王因地制宜,建造了一個三角形形狀的蓄水池,其中頂點分別為A,E,F(E,F兩點在線段BD上),且∠EAF=$\frac{π}{6}$,設∠BAE=α.
小王大學畢業后決定利用所學知識自主創業,在一塊矩形的空地上辦起了養殖場,如圖所示,四邊形ABCD為矩形,AB=200米,AD=200$\sqrt{3}$米,現為了養殖需要,在養殖場內要建造蓄水池,小王因地制宜,建造了一個三角形形狀的蓄水池,其中頂點分別為A,E,F(E,F兩點在線段BD上),且∠EAF=$\frac{π}{6}$,設∠BAE=α.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com