
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | 0 |
分析 先畫出不等式組$\left\{\begin{array}{l}4x+3y-25≤0\\ x-2y+2≤0\\ x-1≥0\end{array}\right.$,對應的平面區域,利用余弦函數在[0,$\frac{π}{2}$]上是減函數,再找到∠POQ最大時對應的點的坐標,就可求出cos∠POQ的最小值.
解答 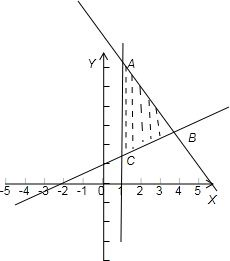 解:滿足不等式組$\left\{\begin{array}{l}4x+3y-25≤0\\ x-2y+2≤0\\ x-1≥0\end{array}\right.$,的平面區域如下圖示:
解:滿足不等式組$\left\{\begin{array}{l}4x+3y-25≤0\\ x-2y+2≤0\\ x-1≥0\end{array}\right.$,的平面區域如下圖示:
因為余弦函數在[0,$\frac{π}{2}$]上是減函數,所以角最大時對應的余弦值最小,
由圖得,當P與A(1,7)重合,Q與B(4,3)重合時,∠POQ最大.
此時kOB=$\frac{3}{4}$,k0A=7.由tan∠POQ=$\frac{7-\frac{3}{4}}{1+7×\frac{3}{4}}$=1⇒∠POQ=$\frac{π}{4}$⇒cos∠POQ=$\frac{\sqrt{2}}{2}$.
故選:A.
點評 本題屬于線性規劃中的延伸題,對于可行域不要求線性目標函數的最值,而是求可行域內的點與原點(0,0)圍成的角的問題.


科目:高中數學 來源: 題型:選擇題
| A. | ①②③ | B. | ①②④ | C. | ②④ | D. | ①②③④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若a1+a2>0,則a1+a3>0 | B. | 若a1+a3>0,則a1+a2>0 | ||
| C. | 若a1>0,則S2017>0 | D. | 若a1>0,則S2016>0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
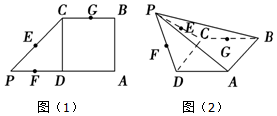 在如圖(1)的平面圖形中,ABCD為正方形,CDP為等腰直角三角形,E、F、G分別是PC、PD、CB的中點,將△PCD沿CD折起,得到四棱錐P-ABCD如圖(2).
在如圖(1)的平面圖形中,ABCD為正方形,CDP為等腰直角三角形,E、F、G分別是PC、PD、CB的中點,將△PCD沿CD折起,得到四棱錐P-ABCD如圖(2).查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
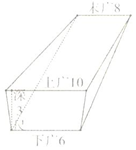 《九章算術》是東方數學思想之源,在卷五《商功》中有以下問題:今有羨除,下廣六尺,上廣一丈,深三尺,末廣八尺,無深,袤七尺,問積幾何?譯文:如圖所示的幾何體是三個側面皆為等腰梯形,其他兩面為直角三角形的五面體,(前端)下寬6尺,上寬一丈,深3尺,末端寬8尺,無深,長7尺,則它的體積是84立方尺.
《九章算術》是東方數學思想之源,在卷五《商功》中有以下問題:今有羨除,下廣六尺,上廣一丈,深三尺,末廣八尺,無深,袤七尺,問積幾何?譯文:如圖所示的幾何體是三個側面皆為等腰梯形,其他兩面為直角三角形的五面體,(前端)下寬6尺,上寬一丈,深3尺,末端寬8尺,無深,長7尺,則它的體積是84立方尺.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
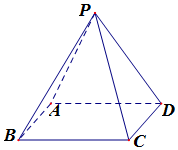 如圖在四棱錐P-ABCD中,底面ABCD為矩形,側面PAD⊥底面ABCD,PA⊥PC;
如圖在四棱錐P-ABCD中,底面ABCD為矩形,側面PAD⊥底面ABCD,PA⊥PC;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com