
 某公司為了準確地把握市場,做好產品生產計劃,對過去四年的數據進行整理得到了第x年與年銷量y(單位:萬件)之間的關系如表:
某公司為了準確地把握市場,做好產品生產計劃,對過去四年的數據進行整理得到了第x年與年銷量y(單位:萬件)之間的關系如表:| x | 1 | 2 | 3 | 4 |
| y | 12 | 28 | 42 | 56 |
分析 (Ⅰ)在圖中畫出表中數據直接畫出散點圖;
(Ⅱ)根據(Ⅰ)中的散點圖擬合y與x的回歸模型,計算y與x的相關系數近似為0.9996,說明y與x的線性相關程度相當,說明可以用線性回歸模型擬合y與x的關系;
(Ⅲ)求出回歸直線方程,然后求解第5年的銷售量.
解答 解:(Ⅰ)作出散點圖如圖:
(Ⅱ)由(Ⅰ)散點圖可知,各點大致分布在一條直線附近,由題中所給表格及參考數據得:$\overline x=\frac{5}{2}$,$\overline y=\frac{69}{2}$,$\sum_{i=1}^4{{x_i}{y_i}=418}$,$\sqrt{\sum_{i=1}^4{{{({y_i}-\overline y)}^2}}}≈32.6$,$\sum_{i=1}^4{x_i^2}=30$,$\sum_{i=1}^4{({x_i}-\overline x)({y_i}-\overline y)=\sum_{i=1}^4{{x_i}{y_i}}-\overline x\sum_{i=1}^4{y_i}=418-\frac{5}{2}×138=73}$,$\sqrt{\sum_{i=1}^4{{{({x_i}-\overline x)}^2}}}=\sqrt{\sum_{i=1}^4{{x_i}^2-n{{\overline x}^2}}}=\sqrt{30-4×{{(\frac{5}{2})}^2}}=\sqrt{5}≈2.24$,$r=\frac{{\sum_{i=1}^4{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sqrt{\sum_{i=1}^4{{{({x_i}-\overline x)}^2}}\sum_{i=1}^4{{{({y_i}-\overline y)}^2}}}}}=\frac{73}{2.24×32.6}≈0.9996$.
∵y與x的相關系數近似為0.9996,說明y與x的線性相關程度相當大,
∴可以用線性回歸模型擬合y與x的關系.
(Ⅲ)由(Ⅱ)知:$\overline x=\frac{5}{2}$,$\overline y=\frac{69}{2}$,$\sum_{i=1}^4{{x_i}{y_i}=418}$,$\sum_{i=1}^4{x^2}=30$,$\sum_{i=1}^4{({x_i}-\overline x}{)^2}=5$,$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}=\frac{73}{5}$,$\widehata=\overline y-\widehatb\overline x=\frac{69}{2}-\frac{73}{5}×\frac{5}{2}=-2$,
故y關于x的回歸直線方程為$\widehaty=\frac{73}{5}x-2$,
當x=5時,$\widehaty=\frac{73}{5}×5-2=71$,
所以第5年的銷售量約為71萬件.
點評 本題考查回歸直線方程的應用,散點圖的畫法,考查計算能力.


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案科目:高中數學 來源: 題型:選擇題
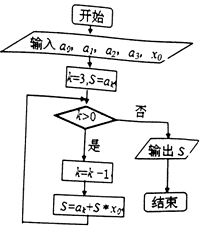 秦九韶是我國南宋時代的數學家,其代表作《數書九章》是我國13世紀數學成就的代表之一;如圖是秦九韶算法的一個程序框圖,則輸出的S為( )
秦九韶是我國南宋時代的數學家,其代表作《數書九章》是我國13世紀數學成就的代表之一;如圖是秦九韶算法的一個程序框圖,則輸出的S為( )| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 參會人數x(萬人) | 11 | 9 | 8 | 10 | 12 |
| 原材料t(袋) | 28 | 23 | 20 | 25 | 29 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ($\frac{3}{4}$,+∞) | B. | [1,+∞) | C. | ($\frac{3}{4}$,1] | D. | {1} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com