
分析 (1)利用三角函數中的恒等變換可化f(x)=2sin(2x+$\frac{π}{3}$),從而可求其周期;
(2)x∈[0,$\frac{5π}{12}$]⇒2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{7π}{6}$],利用正弦函數的單調性可求f(x)在[0,$\frac{5π}{12}$]上的最值.
解答 解:(1)原函數可化為:f(x)=(2sinx+$\sqrt{3}$cosx)cosx-$\sqrt{3}$sin2x
=2sinxcosx+$\sqrt{3}$cos2x=2sin(2x+$\frac{π}{3}$),
∴T=$\frac{2π}{2}$=π,
則f(x)的周期為π;
(2)x∈[0,$\frac{5π}{12}$]⇒2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{7π}{6}$],
∴2sin(2x+$\frac{π}{3}$)∈[-1,2],
∴f(x)在x∈[0,$\frac{5π}{12}$]時,f(x)min=-1,f(x)max=2.
點評 本題考查三角函數中的恒等變換中的應用,考查正弦函數的單調性與最值,屬于中檔題.


科目:高中數學 來源: 題型:解答題
 某公司為了準確地把握市場,做好產品生產計劃,對過去四年的數據進行整理得到了第x年與年銷量y(單位:萬件)之間的關系如表:
某公司為了準確地把握市場,做好產品生產計劃,對過去四年的數據進行整理得到了第x年與年銷量y(單位:萬件)之間的關系如表:| x | 1 | 2 | 3 | 4 |
| y | 12 | 28 | 42 | 56 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在正三棱錐A-BCD中,AB=$\sqrt{5}$,點A到底面BCD的距離為1,E為棱BC的中點.
如圖,在正三棱錐A-BCD中,AB=$\sqrt{5}$,點A到底面BCD的距離為1,E為棱BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| p(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
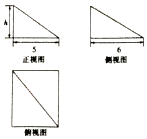
| A. | 8π | B. | 24π | C. | 48π | D. | 64π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①④ | B. | ②③ | C. | ①②③ | D. | ①③④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [2,+∞) | B. | [4,+∞) | C. | [8,+∞) | D. | (0,2] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com