
| A. | [2,+∞) | B. | [4,+∞) | C. | [8,+∞) | D. | (0,2] |
分析 根據(jù)函數(shù)單調(diào)性將不等式進(jìn)行轉(zhuǎn)化結(jié)合絕對(duì)值不等式的性質(zhì)進(jìn)行求最值即可.
解答 解:∵函數(shù)f(x)在R上單調(diào)遞增,
∴若?x∈R,f(|x+1|)≤f(log2a-|x+2|),
等價(jià)為若?x∈R,|x+1|≤log2a-|x+2|成立,
即|x+1|+|x+2|≤log2a成立,
∵|x+1|+|x+2|≥|x+2-x-1|=1,
∴l(xiāng)og2a≥1,即a≥2即可,
故選:A.
點(diǎn)評(píng) 本題主要考查存在性問(wèn)題,根據(jù)函數(shù)單調(diào)性將不等式進(jìn)行轉(zhuǎn)化是解決本題的關(guān)鍵.,注意絕對(duì)值不等式的性質(zhì).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | ($\frac{3}{4}$,+∞) | B. | [1,+∞) | C. | ($\frac{3}{4}$,1] | D. | {1} |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 一條射線 | B. | 兩條射線 | C. | 一條直線 | D. | 兩條直線 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
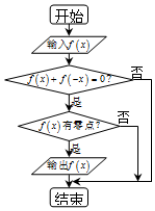 某流程圖如圖所示,現(xiàn)輸入如下四個(gè)函數(shù),則可以輸出的函數(shù)是①②③.
某流程圖如圖所示,現(xiàn)輸入如下四個(gè)函數(shù),則可以輸出的函數(shù)是①②③.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com