
分析 (1)利用函數(shù)奇偶性的定義判斷f(-x)與f(x)的關系,在定義域關于原點對稱的前提下,相等為偶函數(shù),相反為奇函數(shù);
(2)利用導數(shù)與函數(shù)單調性的關系,對函數(shù)求導,通過導數(shù)的符號判斷函數(shù)的單調性;
(3)利用基本不等式以及函數(shù)的單調性求最值.
解答 解:(1)函數(shù)f(x)的定義域為{x|x≠0,x∈R}關于原點對稱
因為f(-x)=-x-$\frac{4}{x}$=-f(x).
所以f(x)是奇函數(shù).
(2)證明:f'(x)=1-$\frac{4}{{x}^{2}}$,f'(x)在區(qū)間(0,2],f'(x)<0,所以在[0,2]是單調減函數(shù),在區(qū)間[2,+∞)上f'(x)>0,所以f(x)在[2,+∞)是單調增函數(shù);
(3)當x∈(0,+∞)時,f(x)≥2$\sqrt{x•\frac{4}{x}}$=4,當且僅當x=2時f(x)取最小值4,無最大值.
點評 本題主要考查函數(shù)的單調性和奇偶性的判斷與證明,同時還考查了利用性質作出函數(shù)圖象,這類作圖不是很準確,但在數(shù)形結合中解決問題很有效


 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:高中數(shù)學 來源: 題型:選擇題
| A. | 6 | B. | -6 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
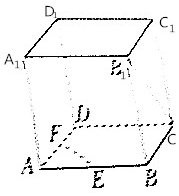 如圖所示,在正方體ABCD-A1B1C1D1中,E、F分別是AB、AD的中點,則異面直線B1C與EF所成的角的大小為( )
如圖所示,在正方體ABCD-A1B1C1D1中,E、F分別是AB、AD的中點,則異面直線B1C與EF所成的角的大小為( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
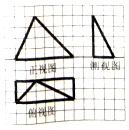 我國南北朝時期數(shù)學家、天文學家祖暅提出了著名的祖暅原理:“冪勢既同,則積不容異”.“勢”即是高,“冪”即是面積.意思是說如果兩等高的幾何體在同高處截得兩幾何體的截面積相等,那么這兩個幾何體的體積相等.已知某不規(guī)則幾何體與如圖所對應的幾何體滿足:“冪勢同”,則該不規(guī)則幾何體的體積為(圖中的網(wǎng)格紙中的小正方形的邊長為1)( )
我國南北朝時期數(shù)學家、天文學家祖暅提出了著名的祖暅原理:“冪勢既同,則積不容異”.“勢”即是高,“冪”即是面積.意思是說如果兩等高的幾何體在同高處截得兩幾何體的截面積相等,那么這兩個幾何體的體積相等.已知某不規(guī)則幾何體與如圖所對應的幾何體滿足:“冪勢同”,則該不規(guī)則幾何體的體積為(圖中的網(wǎng)格紙中的小正方形的邊長為1)( )| A. | 4 | B. | 8 | C. | 16 | D. | 20 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $f(\frac{1}{2})<f(-\frac{3}{2})<f(3)$ | B. | $f(3)<f(-\frac{3}{2})<f(\frac{1}{2})$ | C. | $f(\frac{1}{2})<f(3)<f(-\frac{3}{2})$ | D. | $f(3)<f(\frac{1}{2})<f(-\frac{3}{2})$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com