Question

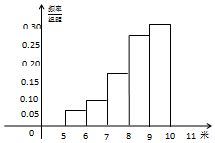
6．某市為了解今年高中畢業生的身體素質狀況，從本市某校高中畢業班中抽取一個班進行實心球測試，成績在8米及以上的為合格．把所得數據整理后，分成六組得到頻率分布直方圖的一部分（如圖）．已知前五個小組的頻率分別為0.06.0.10，0.14，0.28，0.30．第六小組的頻數是6．
（1）求這次測試合格的人數；
（2）用分層抽樣方法在第5、6組的學生中抽取容量為7的一個樣本，將該樣本看作一個總體，從中抽取2人，求恰有一人在第六組的概率．
（3）經過多次測試發現，甲的成績在8～10米之間，乙的成績在9～10米之間現兩人各投一次，求甲投得比乙遠的概率．

Answer 1

分析 （1）由頻率分布直方圖求出第六小組的頻率，再由第六小組的頻數是6，從而求出參加這次測試的學生人數，由此能求出這次測試合格的人數．
（2）由頻率分布直方圖求出第5組和第6組的人數，從而求出用分層抽樣方法在第5、6組的學生中抽取容量為7的一個樣本，第5組和第6組應抽取的人數，將該樣本看作一個總體，從中抽取2人，由此能求出恰有一人在第六組的概率．
（3）設甲、乙各投一次的成績分別為x，y米，基本事件滿足的區域為：$\left\{\begin{array}{l}{8≤x≤10}\\{9≤y≤10}\end{array}\right.$，事件“甲投得比乙遠的概率”滿足的區域為x＞y，由幾何概型能求出甲投得比乙遠的概率．

解答 解：（1）由頻率分布直方圖得到第六小組的頻率為：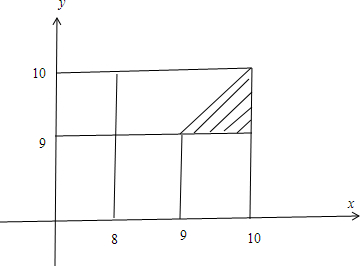
1-（0.06+0.10+0.14+0.28+0.30）
=0.12，
∵第六小組的頻數是6，∴參加這次測試的學生人數n=$\frac{6}{0.12}$=50．
∴這次測試合格的人數為：
（0.28+0.30+0.12）×50=35．
（2）由頻率分布直方圖得第5組有50×0.30=15人，第6組有50×0.12=6人，
用分層抽樣方法在第5、6組的學生中抽取容量為7的一個樣本，
第5組應抽取：7×$\frac{15}{15+6}$=5人，第6組應抽取：7×$\frac{6}{15+6}$=2人，
將該樣本看作一個總體，從中抽取2人，基本事件總數N=${C}_{7}^{2}=21$，
恰有一人在第六組包含的基本事件個數M=${C}_{5}^{1}{C}_{2}^{1}$=10，
∴恰有一人在第六組的概率P=$\frac{M}{N}$=$\frac{10}{21}$．
（3）設甲、乙各投一次的成績分別為x，y米，
則基本事件滿足的區域為：$\left\{\begin{array}{l}{8≤x≤10}\\{9≤y≤10}\end{array}\right.$，
事件“甲投得比乙遠的概率”滿足的區域為x＞y，如圖所示，
由幾何概型知甲投得比乙遠的概率p=$\frac{\frac{1}{2}×1×1}{1×2}$=$\frac{1}{4}$．

點評 本題考查頻率分布直方圖的應用，考查概率的求法，考查推理論證能力、運算求解能力，考查化歸與轉化思想、數形結合思想，是中檔題．