
| A. | |$\overrightarrow{a}$|=1⇒$\overrightarrow{a}$=±1 | B. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$|且$\overrightarrow{a}$∥$\overrightarrow{b}$⇒$\overrightarrow{a}$=$\overrightarrow{b}$ | C. | $\overrightarrow{a}$=$\overrightarrow{b}$⇒$\overrightarrow{a}$∥$\overrightarrow{b}$ | D. | $\overrightarrow{a}$∥$\overrightarrow{0}$⇒|$\overrightarrow{a}$|=0 |
分析 根據(jù)題意,依次分析選項:對于A、由向量模的定義可得A錯誤;對于B、由向量模的定義以及向量平行的性質(zhì)可得B錯誤;對于C、由向量相等的定義分析可得C正確;
對于D、由$\overrightarrow{0}$的性質(zhì),分析可得D錯誤;綜合可得答案.
解答 解:根據(jù)題意,依次分析選項:
對于A、|$\overrightarrow{a}$|=1,即向量$\overrightarrow{a}$的大小為1,$\overrightarrow{a}$=±1沒有意義,故A錯誤;
對于B、|$\overrightarrow{a}$|=|$\overrightarrow{b}$|且$\overrightarrow{a}$∥$\overrightarrow{b}$,說明向量$\overrightarrow{a}$、$\overrightarrow{b}$平行且模相等,則$\overrightarrow{a}$=$\overrightarrow{b}$或$\overrightarrow{a}$=-$\overrightarrow{b}$,故B錯誤;
對于C、$\overrightarrow{a}$=$\overrightarrow{b}$,即向量$\overrightarrow{a}$、$\overrightarrow{b}$相等,其方向相同,必有$\overrightarrow{a}$∥$\overrightarrow{b}$,故C正確;
對于D、$\overrightarrow{a}$∥$\overrightarrow{0}$,$\overrightarrow{0}$與任何向量共線,不能推出|$\overrightarrow{a}$|=0,故D錯誤;
故選:C.
點評 本題考查向量的概念,涉及向量相等、平行以及向量的模等概念,關(guān)鍵是掌握向量的概念.


 課堂練加測系列答案
課堂練加測系列答案 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{3}{10}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
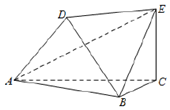 如圖,以A、B、C、D、E為頂點的六面體中,△ABC和△ABD均為等邊三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.
如圖,以A、B、C、D、E為頂點的六面體中,△ABC和△ABD均為等邊三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
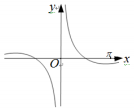
| A. | f(x)=$\frac{{2-{x^2}}}{2x}$ | B. | f(x)=$\frac{cosx}{x^2}$ | C. | f(x)=$\frac{{{{cos}^2}x}}{x}$ | D. | f(x)=$\frac{cosx}{x}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com