
| A. | f(x)=$\frac{{2-{x^2}}}{2x}$ | B. | f(x)=$\frac{cosx}{x^2}$ | C. | f(x)=$\frac{{{{cos}^2}x}}{x}$ | D. | f(x)=$\frac{cosx}{x}$ |
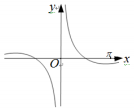
分析 利用函數圖象判斷奇偶性,排除選項,然后利用函數的特殊值判斷即可.
解答 解:由函數的圖象可知函數是奇函數,排除f(x)=$\frac{cosx}{{x}^{2}}$,
x=π時,f(x)=$\frac{{2-{x^2}}}{2x}$=$\frac{2-{π}^{2}}{2π}$<0,
f(x)=$\frac{co{s}^{2}π}{π}$=$\frac{1}{π}>0$,不滿足題意;
f(x)=$\frac{cosπ}{π}$=$-\frac{1}{π}$<0,
因為y=cosx是周期函數,由函數的圖象可知,函數具有波動性,所以函數的解析式可能是D.
故選:D.
點評 本題考查函數的圖象的判斷,解析式的對應關系,考查分析問題解決問題的能力.


 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案科目:高中數學 來源: 題型:選擇題
| A. | |$\overrightarrow{a}$|=1⇒$\overrightarrow{a}$=±1 | B. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$|且$\overrightarrow{a}$∥$\overrightarrow{b}$⇒$\overrightarrow{a}$=$\overrightarrow{b}$ | C. | $\overrightarrow{a}$=$\overrightarrow{b}$⇒$\overrightarrow{a}$∥$\overrightarrow{b}$ | D. | $\overrightarrow{a}$∥$\overrightarrow{0}$⇒|$\overrightarrow{a}$|=0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
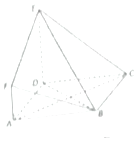 如圖所示,四邊形ABCD為菱形,AF=2,AF∥DE,DE⊥平面ABCD.
如圖所示,四邊形ABCD為菱形,AF=2,AF∥DE,DE⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({-2,\frac{1}{2}})$ | B. | $({-\frac{1}{2},2})$ | C. | (-∞,-2) | D. | $({\frac{1}{2},+∞})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 分值區間 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 頻數 | 20 | 40 | 80 | 50 | 10 |
| 分值區間 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 頻數 | 45 | 75 | 90 | 60 | 30 |

| 女性用戶 | 男性用戶 | 合計 | |
| “認可”手機 | 140 | 180 | 320 |
| “不認可”手機 | 60 | 120 | 180 |
| 合計 | 200 | 300 | 500 |
| P(K2≥x0) | 0.05 | 0.01 |
| x0 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 4 | C. | $2\sqrt{3}$ | D. | $4\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com