
分析 通過Sn≤S5得a5≥0,a6≤0,利用a1=9、a2為整數,由等差數列的通項公式,解不等式可得d=-2,進而可得通項公式;通過an=11-2n,可得bn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(11-2n)(9-2n)}$=$\frac{1}{2}$($\frac{1}{9-2n}$-$\frac{1}{11-2n}$),運用數列的求和方法:裂項相消求和即可得到所求值.
解答 解:在等差數列{an}中,設公差為d,由Sn≤S5得:
可得a5≥0,a6≤0,
又∵a1=9,
∴$\left\{\begin{array}{l}{9+4d≥0}\\{9+5d≤0}\end{array}\right.$,解得-$\frac{9}{4}$≤d≤-$\frac{9}{5}$,
∵a2為整數,∴d=-2,
∴{an}的通項為:an=11-2n;
∴設bn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(11-2n)(9-2n)}$=$\frac{1}{2}$($\frac{1}{9-2n}$-$\frac{1}{11-2n}$),
∴數列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前9項和為T9=$\frac{1}{2}$($\frac{1}{7}$-$\frac{1}{9}$+$\frac{1}{5}$-$\frac{1}{7}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{-9}$-$\frac{1}{-7}$)
=$\frac{1}{2}$(-$\frac{1}{9}$+$\frac{1}{-9}$)=-$\frac{1}{9}$.
故答案為:-$\frac{1}{9}$.
點評 本題考查求數列的通項及求和,考查裂項相消求和法,注意解題方法的積累,屬于中檔題.


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
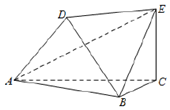 如圖,以A、B、C、D、E為頂點的六面體中,△ABC和△ABD均為等邊三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.
如圖,以A、B、C、D、E為頂點的六面體中,△ABC和△ABD均為等邊三角形,且平面ABC⊥平面ABD,EC⊥平面ABC,EC=$\sqrt{3}$,AB=2.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $-\sqrt{7}$ | B. | 0 | C. | $\sqrt{7}$ | D. | 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
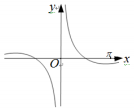
| A. | f(x)=$\frac{{2-{x^2}}}{2x}$ | B. | f(x)=$\frac{cosx}{x^2}$ | C. | f(x)=$\frac{{{{cos}^2}x}}{x}$ | D. | f(x)=$\frac{cosx}{x}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
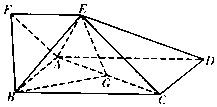 如圖,四邊形ABCD為矩形,四邊形ADEF為梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,點G為AC的中點.
如圖,四邊形ABCD為矩形,四邊形ADEF為梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,點G為AC的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com