
| A. | 2 | B. | 4 | C. | $2\sqrt{3}$ | D. | $4\sqrt{3}$ |
分析 如圖所示,在△ABC中,由余弦定理可得:a2=BC2=$(2\sqrt{7})^{2}+{2}^{2}$-2×$2\sqrt{7}×2×cos∠BAC$=16.解得a.設(shè)∠ADB=α,則∠ADC=π-α.設(shè)AD=m.在△ABD與△ACD中,由余弦定理可得:c2=${m}^{2}+(\frac{a}{2})^{2}$-2m$•\frac{a}{2}$cosα,b2=${m}^{2}+(\frac{a}{2})^{2}$-2m$•\frac{a}{2}$cos(π-α),相加即可得出.
解答 解:如圖所示,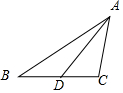
在△ABC中,由余弦定理可得:a2=BC2=$(2\sqrt{7})^{2}+{2}^{2}$-2×$2\sqrt{7}×2×cos∠BAC$
=16.
解得a=4.
設(shè)∠ADB=α,則∠ADC=π-α.設(shè)AD=m.
在△ABD與△ACD中,由余弦定理可得:c2=${m}^{2}+(\frac{a}{2})^{2}$-2m$•\frac{a}{2}$cosα,
b2=${m}^{2}+(\frac{a}{2})^{2}$-2m$•\frac{a}{2}$cos(π-α),
∴c2+b2=2m2+$\frac{{a}^{2}}{2}$,
∴$(2\sqrt{7})^{2}+{2}^{2}$=2m2+$\frac{{4}^{2}}{2}$,
解得m=2$\sqrt{3}$.
故選:C.
點評 本題考查了余弦定理的應(yīng)用、中線長定理,考查了推理能力與計算能力,屬于中檔題.


科目:高中數(shù)學(xué) 來源: 題型:選擇題
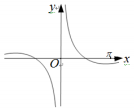
| A. | f(x)=$\frac{{2-{x^2}}}{2x}$ | B. | f(x)=$\frac{cosx}{x^2}$ | C. | f(x)=$\frac{{{{cos}^2}x}}{x}$ | D. | f(x)=$\frac{cosx}{x}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題

| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
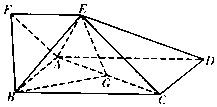 如圖,四邊形ABCD為矩形,四邊形ADEF為梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,點G為AC的中點.
如圖,四邊形ABCD為矩形,四邊形ADEF為梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,點G為AC的中點.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 4 | B. | 5 | C. | ±4 | D. | ±5 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | (1)(3) | B. | (1)(4) | C. | (2)(3) | D. | (2)(4) |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com